Deep Learning: Difference between revisions
| Line 563: | Line 563: | ||
===Neural Networks=== | ===Neural Networks=== | ||
Consider a two-layer neural network.<br> | Consider a two-layer neural network.<br> | ||
We can write the output as: | We can write the output as:<br> | ||
<math>y = f(w, x) = \frac{1}{\sqrt{m}} \sum_{i=1}^{m} b_i \sigma(a_i^t x)</math><br> | <math>y = f(w, x) = \frac{1}{\sqrt{m}} \sum_{i=1}^{m} b_i \sigma(a_i^t x)</math><br> | ||
We use quadratic loss: <math>L(w) = \frac{1}{2} \sum_{i=1}^{n} (f(w, x_i) - y_i)^2</math><br> | We use quadratic loss: <math>L(w) = \frac{1}{2} \sum_{i=1}^{n} (f(w, x_i) - y_i)^2</math><br> | ||
GD: <math>w(t+1) = w(t) - \eta_{t} \sum_{i=1}^{n} (f(w, x_i) - y_i) \nabla_w f(w_t, x_i)</math> | GD: <math>w(t+1) = w(t) - \eta_{t} \sum_{i=1}^{n} (f(w, x_i) - y_i) \nabla_w f(w_t, x_i)</math> | ||
# Init N(0,1) | # Init N(0,1) | ||
# Our weights update along a trajectory: w(0), w(1), ... | # Our weights update along a trajectory: w(0), w(1), ... | ||
# Each <math>w</math> is a weight matrix. | # Each <math>w</math> is a weight matrix. | ||
Empirical Observation: When the width of the network <math>m</math> is large, the trajectory of the gradient descent is ''almost'' static. | Empirical Observation: When the width of the network <math>m</math> is large, the trajectory of the gradient descent is ''almost'' static. | ||
This is called ''lazy'' training. | This is called ''lazy'' training. | ||
* Not always the case! Especially for small <math>m</math>. | * Not always the case! Especially for small <math>m</math>. | ||
Since the change in the model weights are not large, we can write the first-order taylor approximation: | Since the change in the model weights are not large, we can write the first-order taylor approximation:<br> | ||
<math>f(w, x) \approx f(w_0, x) + \nabla_{w} f(w_0, x)^t (w - w_x) + ...</math><br> | <math>f(w, x) \approx f(w_0, x) + \nabla_{w} f(w_0, x)^t (w - w_x) + ...</math><br> | ||
This model is linear in <math>w</math>.<br> | This model is linear in <math>w</math>.<br> | ||
<math>\phi(x) = \nabla_{w} f(w_0, x)</math><br> | <math>\phi(x) = \nabla_{w} f(w_0, x)</math><br> | ||
The kernel <math>K = \langle \phi(x_i), \phi(x_j) \rangle</math> is called the ''Neural Tangent Kernel'' (NTK). | The kernel <math>K = \langle \phi(x_i), \phi(x_j) \rangle</math> is called the ''Neural Tangent Kernel'' (NTK). | ||
These features will not change during the optimization process because we use <math display="inline">w_0</math> | |||
Go back to our 2-layer NN:<br> | Go back to our 2-layer NN:<br> | ||
Latest revision as of 16:18, 3 March 2022
Notes for CMSC 828W: Foundations of Deep Learning (Fall 2020) taught by Soheil Feizi.
Basics
A refresher of Machine Learning and Supervised Learning.
Empirical risk minimization (ERM)
Minimize loss function over your data: \(\displaystyle \min_{W} \frac{1}{N} \sum_{i=1}^{N} l(f_{W}(x_i), y_i))\)
Loss functions
For regression, can use quadratic loss: \(\displaystyle l(f_W(x), y) = \frac{1}{2}\Vert f_W(x)-y \Vert^2\)
For 2-way classification, can use hinge-loss: \(\displaystyle l(f_W(x), y) = \max(0, 1-yf_W(x))\)
For multi-way classification, can use cross-entropy loss:
\(\displaystyle g(z)=\frac{1}{1+e^{-z}}\)
\(\displaystyle \min_{W} \left[-\sum_{i=1}^{N}\left[y_i\log(y(f_W(x_i)) + (1-y_i)\log(1-g(f_W(x_i))\right] \right]\)
Nonlinear functions
Given an activation function \(\phi()\), \(\phi w^tx + b\) is a nonlinear function.
Models
Multi-layer perceptron (MLP): Fully-connected feed-forward network.
Optimization
Apply gradient descent or stochastic gradient descent to find \(W^*\).
Stochastic GD:
- Sample some batch \(B\)
- \(w^{(t+1)} = w^{(t)} - \eta \frac{1}{|B|} \sum_{i \in B} \nabla_{W} l(f_{W}(x_i), y_i)\)
Optimizers/Solvers:
- Momentum
- RMSProp
- Adam
DL Optimization
(Lectures 2-3, September 3)
The role of "over-parameterization".
In general, you can have poor local minimums and saddle points (with pos+neg Hessian).
However, in practice GD & SGD work pretty well.
Lecture 2 (Sept 3) is about Liu et al. [1].
Suppose we have a classification problem with \(c\) labels and \(N\) samples total. This gives us \(n=N*c\) constraints.
Interpolation is possible if the number of parameters \(m\) is greater than the number of samples \(n=N*c\).
This is called the over-parameterized regime.
In the exact interpolation regime, we have: \[ \begin{aligned} f_W(x_1) &= y_1 = \begin{bmatrix} 0 \\ \vdots \\ 1 \end{bmatrix} \in \mathbb{R}^c\\ &\vdots\\ f_W(x_1) &= y_1 = \begin{bmatrix} 0 \\ \vdots \\ 1 \end{bmatrix} \in \mathbb{R}^c\\ \end{aligned} \] This can be rewritten as \(\displaystyle F(w)=y\) where x is implicit.
In the under-parameterized regime, we get poor locals. (See Fig 1a of [1]).
The poor-locals are locally convex in the under-parameterized regime but not in the over-parameterized.
Over-parameterized models have essential non-convexity in their loss landscape.
Minimizers of convex functions form convex sets.
Manifold of \(w^*\) have some curvature.
Manifold of \(w^*\) should be an affine subspace. This is in general for non-linear functions.
So we cannot rely on convex analysis to understand over-parameterized systems.
Instead of convexity, we use PL-condition (Polyak-Lojasiewicz, 1963):
For \(\displaystyle w \in B\), \(\displaystyle \frac{1}{2}\Vert \nabla L(w) \Vert^2 \geq \mu L(w)\) which implies exponential (linear) convergence of GD.
Tangent Kernels
Suppose our model is \(F(w)=y\) where \(w \in \mathbb{R}^m\) and \(y \in \mathbb{R}^n\).
Then our tangent kernel is:
\[K(w) = \nabla F(w) \nabla F(w)^T \in \mathbb{R}^{n \times n}\]
where \(\nabla F(w) \in \mathbb{R}^{n \times m}\)
Theorem 4.1 (Uniform conditioning implies PL* condition)
If \(\lambda_{\min} (K(w)) \geq \mu\) then \(\mu\text{-PL*}\) on \(B\).
Informal convergence result:
GD converges exp fast to a solution with the rate controlled by a condition number:
\[ \kappa_{F} = \frac{\sup_{B} \lambda_{\max}(H)}{\inf_{B} \lambda_{\min}(K)}\]
Ideally we want this to be small.
Theorem 4.2 (Local PL* implies existence of a solution + fast convergence)
Assume \(\displaystyle L(w)\) is \(\beta\)-smooth and satisfies \(\mu\)-PL condition around a ball \(\displaystyle B(w_0, R)\) with \(\displaystyle R = \frac{2\sqrt{w\beta L(w_0)}{\mu}\). Then:
- Existence of a solution: There exists a global minimum of \(\displaystyle L\), \(\displaystyle \mathbf{w}^* \in B(\mathbf{w}_0, R)\) s.t. \(\displaystyle F(\mathbf{w}^*)=\mathbf{y}\).
- Convergence of GD: GD with step size \(\displaystyle \eta = 1/\sup_{\mathbf{w}}\lambda_{\max}(H)\) converges with exponential convergence rate:
- \[L(w_t) \leq \left(1-\kappa^{-1}(B(\mathbf{w}, R))\right)^t L(\mathbf{w}_0)\]
Beginning of Lecture 3 (September 8, 2020)
Last time (lecture 2) we expect zero training error from overparameterization.
This is the interpolation regime.
Here the number of parameters \(m\) is greater than the number of samples \(n=Nc\).
Here the manifold of \(w^*\) is the intersection of functions where \(F(w, x_1)=Y_1\) and \(F(w,x_2)=Y_2\).
Assume we use squared loss \(L(w)=\frac{1}{2}\Vert F(w)-Y \Vert^2\).
In general, our loss function is non convex, even locally.
PL-condition: If the magnitude of gradient is greater than a constant multiple \(\mu\) of loss then we say it is \(\mu\)-PL.
If our loss satisfies PL and some other conditions, then it will converge with gradient descent.
Intuition of PL
Assume:
- Loss \(\displaystyle L(w)_{w \in B}\) is \(\mu\)-PL
- Loss is \(\beta\)-smooth
- The hessian is bounded by \(\beta\)
- \(\eta=\frac{1}{\beta}\)
- Assume gradient descent: \(w_{t+1}=w_t-\mu \nabla L(w_t)\)
By Taylor's expansion:
\[
\begin{aligned}
L(w_{t+1}) &= L(w_t) + (w_{t+1}-w_t)^T \nabla f(w_t) + \frac{1}{2}(w_{t+1}-w_t)^T H(w')(w_{t+1}-w_{t})\\
&=L(w_t) + (-\eta)\nabla L(w_t)^T \nabla f(w_t) + \frac{1}{2}(-\eta)\nabla L(w_t)^T H(w')(-\eta) \nabla L(w_t)\\
&\leq L(w_t) - \eta \Vert \nabla L(w_t) \Vert^2 + \frac{\eta^2}{2} \nabla L(w_t)^T H(w') \nabla L(w_t)\\
&\leq L(w_t) - \eta \Vert \nabla L(w_t) \Vert^2 (1-\frac{\eta \beta}{2}) &\text{by assumption 3}\\
&\leq L(w_t) - \frac{\eta}{2} \Vert \nabla L(w_t) \Vert^2 &\text{by assumption 4}\\
&\leq L(w_t) - \eta \mu L(w_t) &\text{by }\mu\text{-PL assumption}\\
&= (1-\eta \mu)L(w_t)
\end{aligned}
\]
This implies our loss at any iteration is \(\displaystyle L(w_t) \leq (1-\eta \mu)^t L(w_0)\).
Thus we see a geometric or exponential decrease in our loss function with convergence rate \(\displaystyle (1-\eta \mu)\).
Similar results hold for SGD.
Caveat:
Here we assume our loss is in a ball \(\displaystyle B(w_0, R) = \{w | \Vert w - w_0 \Vert \leq R\}\) where \(\displaystyle R \leq \frac{2\sqrt{2 \beta L(w_0)}}{\mu}\).
We need to show that our gradient updates never causes us to leave this ball.
The lengths of the update vectors are \(\displaystyle \Vert w_{t+1} - w_{t}\Vert = \eta \Vert \nabla L(w_t)\Vert\).
To show that we never leave the ball, we need to have an upper bound on the length of our gradients \(\displaystyle \Vert \nabla L(w_t) \Vert\).
There is a tradeoff because for PL, we want a large \(\displaystyle \mu\) to lower bound the gradients but that would require satisfying PL over a large ball. If \(\displaystyle \mu\) is small, then we have fast (large) updates but over a small ball.
From the proof above, we have:
\(\displaystyle L(w_{t+1}) \leq L(w_t) - \frac{\eta}{2} \Vert \nabla L(w_t) \Vert^2\).
We can use this to prove we are in the ball.
Why do neural networks satisfy the conditioning assumptions?
Hessian Control
We can show \(mu\)-PL by showing the smallest eigenvalue of the tangent kernel is bounded: \(\displaystyle \lambda_{\min}(K(w_0)) \geq \mu\) and \(\displaystyle \sup_{B} \Vert H(F)\Vert\).
The tangent kernel is \(\displaystyle \nabla F(w) \nabla F(w)^T\).
If hessian is bounded then gradients don't change too fast so if we are \(\displaystyle \mu\)-PL at the initialization then we are \(\displaystyle \mu\)-PL in a ball around the initialization.
Suppose we have a NN: \(\displaystyle x \in \mathbb{R} \to y\).
\(\displaystyle f(w, x) = \frac{1}{\sqrt{m}}\sum_{i=1}^{m} v_i \sigma(w_i, x)\).
- Can we prove convergence of GD for this NN?
\(\displaystyle \nabla_{w_i} f(w, x) = \frac{1}{\sqrt{m}} v_i x \sigma'(w_i x)\)
\(\displaystyle K(w, x_j, x_j) = \frac{1}{m}\sum_{i=1}^{m} v_i^2 x^2 \left(\sigma'(w_i x)\right)^2 \equiv O(1)\) are the j-th diagonal terms of the tangent kernel:
\(\displaystyle K(w) \in \mathbb{R}^{n \times n}\).
Then the trace of the tangent kernel is also \(\displaystyle O(1)\) so the eigenvalues are bounded: \(\displaystyle \Vert K(w) \Vert = O(1)\).
\(\displaystyle H_{ij} = \frac{1}{\sqrt{m}} v_i \sigma '' (w_j x) x^2 1_{i=j}\)
The hessian is a diagonal matrix. The spectral norm of the hessian (the maximum eigenvalue) is the maximum of the diagonal elements:\\
\(\displaystyle \Vert H \Vert_2 = \max_{i \in [m]} H_{ii} = \frac{x^2}{\sqrt{m}} \max_{i \in [m]} | v_i \sigma '' (w_j x)| = O(\frac{1}{\sqrt{m}})\)
As m goes to infinity, our hessian \(\displaystyle H\) goes to 0 and tangent kernel \(\displaystyle K\) goes to a constant.
Thus Hessian control implies convergence of GD/SGD.
- However this argument assumes the model is almost linear.
- This hessian control can be extended to L-layer NN with \(\displaystyle m=\omega(\frac{n}{\mu})\)
Example:
\(\displaystyle g(w, x) = \phi(\frac{1}{\sqrt{m}}\sum_{i=1}^{m}v_i \sigma(w_i x))\)
then
- \(\displaystyle \Vert K(w) \Vert = O(1)\)
- \(\displaystyle \Vert H \Vert = O(1)\) if \(\displaystyle (\phi'' \neq 0)\)
so we cannot use hessian control.
- Lemma
If f is mu-PL then \(\displaystyle \phi \circ f\) is \(\displaystyle \mu \rho^2\)-PL (\(\displaystyle | \phi'(f(w,x))| \gt \phi\)).
implies \(\displaystyle L(w_t) \leq (1- \eta \mu \rho^2)L(w_0)\).
GD converges even though our model does not go to a linear model.
Takeaway
Over-parameterization does not lead to linearization. Over-parameterization leads to good conditioning which leads to PL and convergence of GD/SGD.
Other papers:
- Simon Du et al.[2]
Start of Lecture 4 (Sept 10)
This lecture is about Soudry et al.[3].
Setup:
- Binary classification
- Data is linearly separable
- No bias term (b=0)
Why do we pick \(w^*\) to be the max-margin solution?
To have better generalization.
We will consider functions \(f_w(x) = w^t x\) where we have \(\{(x_i, y_i)\}_{1}^{N}\), \(f_w: \mathbb{R}^d \to \mathbb{R}\), \(x_i \in \mathbb{R}^d\) and \(y_i \in \{-1, 1\}\).
We can use one of the loss functions:
- hinge loss \(l(x)=\max(1-x, 0\))
- logistic loss \(l(u) = \log(1+e^{-u})\)
- exp loss \(l(u)=e^{-u}\)
Our overall loss will be the sum of loss for each sample:
\(L(w) = \sum_{u=1}^{N}l(y_i w^t x_i)\)
Here \(x_i\) and \(y_i\) are constants so call \(\tilde{x}_i = y_i x_i\).
Now our loss is \(L(w) = \sum_{u=1}^{N}l(w^t \tilde{x}_i)\)
Assumptions:
- Data is linearly separable: \(\exists w^* \) s.t. \((w^*)^t x_i > 0\).
- \(l(u)\) is positive, differentiable, monotonically decreasing to 0, and \(\beta\)-smooth.
- Logistic and exp loss satisfy assumption 2.
Hard SVM:
Call the SVM solution \(w_{svm}^t x = 0\).
Recall the SVM optimization is:
\(\displaystyle
\begin{aligned}
\min &\Vert w \Vert^2\\
&w^t x_i \geq 1 \; \forall i
\end{aligned}
\)
We use GD to find \(w^*\):
\(\min \sum_{i=1}^{N} l(w^t x_i)\)
\(\displaystyle
\begin{aligned}
w(t+1) &= w(t) - \eta \nabla L(w(t))\\
&= w(t) - \eta \sum_{i=1}^{N} l'(w^t x_i) x_i
\end{aligned}
\)
Since the data is linearly separable, there exists \(w^*\) such that:
\((w^*)^t \nabla L(w) = \sum_{i=1}^{N} l'(w^t x_i) x_i^t w^* < 0\)
Here \(l'(w^t x_i) > 0\) and \(x_i^t w^* < 0\).
This implies there are no finite critical points (where \(\nabla L(w) = 0\).
But GD on a smooth loss converges to a critical point.
This implies \(\Vert w(t) \Vert\) goes to infinity and the loss converges to 0.
Since the loss converges to 0, GD converges to a global min.
Assumption 3: Loss function has exponential tails.
Exp and logistic loss satisfy this assumption.
- Theorem
Under assumptions 1-3, GD behaves as:
\(\displaystyle w(t) = w_{svm} \log(t) + \rho(t)\) where \(\displaystyle \Vert \rho(t) \Vert = o(\log \log t)\).
This implies \(\displaystyle \lim_{t \to \infty} \frac{w(t)}{\Vert w(t) \Vert} = \frac{w_{svm}}{\Vert w_{svm} \Vert}\).
Rate of convergence is very slow:
\(\displaystyle \left\Vert \frac{w(t)}{\Vert w(t) \Vert} - \frac{w_{SVM}}{\Vert w_{SVM} \Vert } \right\Vert = O(\frac{1}{\log(t)})\)
Takeaway
- Even when the loss is very small, if we continue GD optimization we approach the max-margin solution which improves generalization.
- Validation or test loss may go to infinity \(\displaystyle \Omega(\log (t))\). It is better to look at the classification error in test/validation rather than the pure loss value.
- Even if validation loss is increasing, you should not stop GD because it will approach max-margin.
- More recent work
- Implicit bias exists in over-parameterized neural networks.
- Experimentally, Adam and Adagrad do not have implicit bias but have worse generalization error.
DL Generalization
Beginning of Lecture 5 (September 15, 2020).
Training set \(S = \{z^{(i)} = (x^{(i)}, y^{(i)}) \}_{i=1}^{n}\).
Our samples are from some unknown distribution: \(Z^{(i)} = (x^{(i)}, y^{(i)}) \sim P_{X, Y}\).
\(\min_{h \in H} L_{S}(h) \to h_{S}^{*}\)
In practice, we cannot compute our population loss: \(\displaystyle L_{D}(h) = E_{z \in P_{X, Y}} [l(h, z)]\).
\(\displaystyle \min{h \in H} L_{D}(h) \to h_{D}^*\).
The goal is to learn something from the training set which has a low population loss.
The estimation error is \(\displaystyle L_{D}(h_{S}^*) - L_{D}(h_{D}^*)\) where \(\displaystyle L_{D}(h_s^*)\) is the true population loss of the hypothesis gained from the test set and \(\displaystyle L_{D}(h_D^*)\) is the minimum population loss.
Classical Learning Theory
If \(\displaystyle \forall P_{X, Y}, n \geq n_0\), \(\displaystyle Pr(L_{D}(h_{S}^*) - L_{D}(h_{D}^*) \leq \epsilon) \geq 1-\delta\) then is H called PAC-learnable.
Bias-variance tradeoff
\(\displaystyle L_{D}(h_{S}^*) = L_{D}(h_{D}^*) + [L_{D}(h_{S}^*) - L_{D}(h_{D}^*)]\)
- \(\displaystyle L_{D}(h_{D}^*)\) is called the bias term, the loss of the best hypothesis in your hypothesis class. If the complexity of \(\displaystyle H\) increases, then the bias term will decrease.
- \(\displaystyle L_{D}(h_{S}^*) - L_{D}(h_{D}^*)\) is the estimation error or variance term.
- As the complexity of \(\displaystyle H\) increases, the bias decreases but the variance increases.
However, this view is not complete.
- Notations
\(\displaystyle f = l \circ h\)
\(\displaystyle L_{S}(h) = \frac{1}{n} \sum_{i=1}^{n} f(z^{(i)})\)
\(\displaystyle L_{D}(h) = E_{Z \sim P_{X, Y}}[ f(z) ] \)
\(\displaystyle F = l \circ H = \{ l \circ h, \forall h \in H \}\)
\(\displaystyle F \circ S = \left\{
\begin{bmatrix}
f(z^{(1)})\\
\vdots\\
f(z^{(n)})
\end{bmatrix}, \forall f \in F \right\}\)
Generalization error: \(\displaystyle L_{D}(h_{S}^*) - L_{S}(h_{S}^*)\)
We want to have a uniform bound on this error: \(\displaystyle G = \sup_{h \in H} L_{D}(h) - L_{S}(h)\).
We don't have the population distribution \(\displaystyle D\).
Instead, what we do is split the training data: \(\displaystyle S = S_1, \cup S_2\) with \(\displaystyle |S_1|=|S_2|=\frac{n}{2}\).
Now we have:
\(\displaystyle
\begin{aligned}
G \approx G' &=\sup_{h \in H} L_{S_1}(h) - L_{S_2}(h)\\
&= \sup_{h \in H} F(s_1) - F(s_2)\\
&= \sup_{h \in H} \frac{1}{n/2} \sum_{z^{(i)} \in S_1} f(z^{(i)}) - \frac{1}{n/2} \sum_{z^{(i)} \in S_1} f(z^{(i)})\\
&= \sup_{h \in H} \frac{2}{n} \sum_{i=1}^{n} \sigma_i f(z^{(i)}) & \text{where }\sigma_{i} = I[z^{(i)} \in S_1] - I[z^{(i)} \in S_2]
\end{aligned}
\)
We can use randomized partitioning such that \(\displaystyle \sigma = \begin{cases} 1 & \text{w.p. }1/2\\ -1 & \text{w.p. }1/2 \end{cases} \)
\(\displaystyle G \approx E_{\sigma}[G'] = \frac{2}{n} E_{\sigma} \left[ \sup_{h \in H} \sum_{i=1}^{n} \sigma_i f(z^{(i)}) \right]\)
\(\displaystyle R(A) = \frac{1}{n} E_{\sigma} \left[ \sup _a \in A \sum_{i=1}^{n} \sigma_i a_i \right]\) is called the Rademacher complexity.
Setting \(\displaystyle A = \{a_i\} = F \circ S\) \(\displaystyle \implies G \approx 2 R(F \circ S)\)
Theorem
With probability \(\displaystyle 1 - \delta\),
\(\displaystyle L_D(h) - L_{S}(h) \leq 2 R(F \circ S) + c \sqrt{\frac{\log(4/\delta)}{n}}\)
Example: \(\displaystyle H = \{ h(x) = w^t x, \Vert w \Vert_2 \leq 1\}\)
\(\displaystyle R(H \circ S) \leq \frac{\max_i \Vert x^{(i)} \Vert_2}{\sqrt{n}}\)
Question: What is the Rademacher complexity of a deep model?
\(\displaystyle H = \{ h(x) \mid h \text{ is a NN with some structure}\}\)
If \(\displaystyle R(H \circ S)\) is small then by the theorem, we can have good generalization performance.
Zhang et al.[4] perform a randomization test.
They assign random labels and observe that neural networks can fit random labels.
Recall \(\displaystyle R(H \circ S) = \frac{1}{n} E_{\sigma} \left[ \sup_{h \in H} \sum_{i=1}^{n} \sigma_i h(x_i) \right] \approx 1\)
This shows that Rademacher complexity and VC-dimension are not useful for explaining generalization for neural networks.
Universal Approximation Theorem
There exists a two-layer NN with Relu activations and \(\displaystyle 2n+d\) parameters that can represent any function on a sample size \(\displaystyle n\) in d dimensions.
Lecture 9 (Sept 17)
From previous lecture (Zhang et al.[4]), we see that NN optimization is not much more difficult training on random labels in terms of convergence rate. Thus, Rademacher complexity and VC dimension cannot explain generalization by itself.
Examples of explicit regularization:
- Data augmentation (e.g. random crop)
- Weight decay (L2 regularization on parameters)
- Dropout
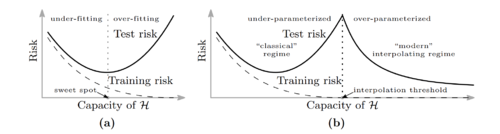
These types of explicit regularization improves generalization, but models still generalize well without them.
One reason would be implicit regularization by SGD.
Belkin et al.[5] observe that as models get more over-parameterized in the interpolation regime, test error will begin decreasing with the number of parameters. This is called double descent.
- Intuition
- In the over-parameterized regime, there are infinitely many solutions in the manifold of \(\displaystyle f_{w^*}\).
For SGD, it is easier to find simple solutions (e.g. functions with small norms). This leads to better generalization.
Can we analyze the double descent curve for some simple distributions or models?
Setup:
Our features are \(\displaystyle x = (x_1,..., x_d)\) where \(\displaystyle x_i\) are from standard normal.
Our labels are \(\displaystyle y = x^t \beta\). This is the noise-free case.
Our training set: \(\displaystyle \{(x^{(i)}, y^{(i)})\}_{i=1}^{n}\) written as \(\displaystyle X =
\begin{pmatrix}
(x^{(1)})^t\\
\vdots\\
(x^{(n)})^t
\end{pmatrix}
\)
Learning: We select \(\displaystyle p\) features: \(\displaystyle T \subseteq [d]\), \(\displaystyle |T| = P\) and fit a linear model \(\displaystyle \beta^{*}_{T} \in \mathbb{R}^{p}\), \(\displaystyle \beta^*_{T^c} =0\). Here \(\displaystyle T^c\) is the set of features we are not using.
Define \(\displaystyle X_{T} = \begin{pmatrix} (x^{(1)}_T)^t\\ \vdots\\ (x^{(n)}_T)^t \end{pmatrix} \in \mathbb{R}^{n \times P} \)
Quadratic loss: \(\displaystyle \min_{\beta_T} \Vert X_T \beta_T - y \Vert_{2}^{2} \in \mathbb{R}\).
The optimal solution is \(\displaystyle \beta_{T}^* = (X_{T}^t X_{T})^{-1} X_{T}^t y = X_{T}^{+} y\) where \(\displaystyle X_{T}^{+}\) is the Moore-penrose Pseudo-inverse.
Since we know \(\displaystyle P_{X, Y}\), we can compute the generalization error exactly.
\(\displaystyle
\begin{aligned}
E_{X,Y} \left[(y - x^t \beta^*)^2 \right] &= E \left[(x^t(\beta - \beta^*))^2\right]\\
&= E \left[(\beta - \beta^*)^t x x^t (\beta - \beta^2)\right]\\
&= (\beta - \beta^*)^t E \left[ x x^t \right] (\beta - \beta^2)\\
&= \Vert \beta - \beta^* \Vert\\
&= \Vert \beta_{T^c} \Vert^2 + \Vert \beta_{T} - \beta_{T}^* \Vert^2
\end{aligned}
\)
- Theorem
- \(\displaystyle B_{T^c} \neq 0\)
\(\displaystyle E \left[(y - x^t \beta^*)^2 \right] = \begin{cases} \Vert B_{T^C} \Vert^2 (1 + \frac{p}{n-p-1}) & p \leq n-2\\ +\infty & n-1 \leq p \leq n+1\\ \Vert B_{T} \Vert ^2 (1 - \frac{n}{p}) + \Vert B_{T^c} \Vert^2 (1 + \frac{n}{p-n-1}) & p \geq n+2 \end{cases} \)
In other cases, prescient feature selection. We can include features in \(\displaystyle T\) by decreasing the order of \(\displaystyle \beta_j^2 = \frac{1}{j^2}\). From this we get a behavior like double descent.
Related Works
Jiang et al.[6] provide some emperical evaluations of different generalization bounds such as:
- Sharpness-based bounds (PAC-Bayesian)
- Norm-based bounds
Neural Tangent Kernels (NTKs)
Beginning of Lecture 7 (Sept. 22, 2020)
Linear Regression
Assume we have a dataset:
\(\displaystyle \{(x_i, y_i)\}_{i=1}^{n}\)
\(\displaystyle y_i \in \mathbb{R}\)
\(\displaystyle x_i \in \mathbb{R}^d\)
\(\displaystyle f(w, x) = w^t x\)
\(\displaystyle L(w) = \frac{1}{2} \sum_{i=1}^{n}(y_i - f(w, x_i))^2\)
\(\displaystyle \min_{W} L(w)\)
GD: \(\displaystyle w(t+1) = w(t) - \eta_{t} \nabla L(w_t)\) where our gradient is:
\(\displaystyle \sum_{i=1}^{n}(y_i - f(w, x_i)) \nabla_{w} f(w_t, x_i) = \sum_{i=1}^{n}(y_i - f(w, x_i)) x_i\)
Kernel Method
\(\displaystyle x_i \in \mathbb{R}^d \to \phi(x_i) \in \mathbb{R}^{D}\) with \(\displaystyle D \gt \gt d\)
Suppose \(\displaystyle d=3\) and \(\displaystyle x = \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} \to \phi(x)= \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_1 x_2\\ x_1 x_3\\ x_2 x_3 \end{bmatrix} \)
\(\displaystyle f(w, x) = w^t \phi(x)\)
Is this model linear in w? Yes!
Is this model linear in x? No!
\(\displaystyle \min \frac{1}{2} \sum_{i=1}^{n} (y_i - w^t \phi(x_i))^2\)
Apply GD or convex optimization.
Q: What is the issue here?
- \(\displaystyle \phi\) is fixed!
- \(\displaystyle D = O(d^k)\)
- For ImageNet, \(d\) is approx \(10^5\) so \(D=O(10^{15})\)
- Kernel Trick
We may have a closed form solution for \(\displaystyle \langle \phi(x_i), \phi(x_j) \rangle\).
This is called the kernel function \(\displaystyle K(x_i, x_j)\) or kernel matrix \(\displaystyle K \in \mathbb{R}^{n \times n}\).
\(K\) is a PSD matrix.
Idea: In many cases without "explicit" comp of \(\displaystyle \phi(x_i)\), we can compute \(\displaystyle K(x_i, x_j)\).
- Polynomial Kernels
\(\displaystyle K(x_i, x_j) = (x + x_i^t x_j)^k\) with \(\displaystyle \phi(x_i) \in \mathbb{R}^D\)
Here \(\displaystyle D=O(d^k)\) but \(\displaystyle K(x_i, x_j)\) is \(\displaystyle O(d)\).
Many classical techniques can be kernelized:
- SVM to Kernel SVM
- Ridge regression to Kernel ridge regression
- PCA to Kernel PCA
Neural Networks
Consider a two-layer neural network.
We can write the output as:
\(\displaystyle y = f(w, x) = \frac{1}{\sqrt{m}} \sum_{i=1}^{m} b_i \sigma(a_i^t x)\)
We use quadratic loss: \(\displaystyle L(w) = \frac{1}{2} \sum_{i=1}^{n} (f(w, x_i) - y_i)^2\)
GD: \(\displaystyle w(t+1) = w(t) - \eta_{t} \sum_{i=1}^{n} (f(w, x_i) - y_i) \nabla_w f(w_t, x_i)\)
- Init N(0,1)
- Our weights update along a trajectory: w(0), w(1), ...
- Each \(\displaystyle w\) is a weight matrix.
Empirical Observation: When the width of the network \(\displaystyle m\) is large, the trajectory of the gradient descent is almost static. This is called lazy training.
- Not always the case! Especially for small \(\displaystyle m\).
Since the change in the model weights are not large, we can write the first-order taylor approximation:
\(\displaystyle f(w, x) \approx f(w_0, x) + \nabla_{w} f(w_0, x)^t (w - w_x) + ...\)
This model is linear in \(\displaystyle w\).
\(\displaystyle \phi(x) = \nabla_{w} f(w_0, x)\)
The kernel \(\displaystyle K = \langle \phi(x_i), \phi(x_j) \rangle\) is called the Neural Tangent Kernel (NTK).
These features will not change during the optimization process because we use \(w_0\)
Go back to our 2-layer NN:
\(\displaystyle f_m(w, x) = \frac{1}{\sqrt{m}} \sum b_i \sigma(a_i^t x)\)
\(\displaystyle \nabla_{a_i} f_m(w, x) = \frac{1}{\sqrt{m}} b_i \sigma'(a_i^t x) x\)
\(\displaystyle \nabla_{b_i} f_m(w, x) = \frac{1}{\sqrt{m}} \sigma(a_i^t x)\)
\(\displaystyle K_{m}(x, x') = K_{m}^{(a)}(x, x') + K_{m}^{(b)}(x, x')\)
\(\displaystyle K_{m}^{(a)}(x, x') = \frac{1}{m} \sum_{i=1}^{m} b_i^2 \sigma'(a_i^tx) \sigma'(a_i^tx) (x x')\)
\(\displaystyle K_{m}^{(b)}(x, x') = \frac{1}{m} \sum_{i=1}^{m} \sigma(a_i^t x) \sigma(a_i^t x')\)
- \(\displaystyle a_i\) and \(\displaystyle b_i\) are independent samples at initialization.
Based on law of large numbers, as m goes to infinity,
\(\displaystyle K_{m}^{(a)}(x, x') \to K^{(a)}(x, x') = E \left[ b^2 \sigma'(a^t x) \sigma'(a^t x') (x x') \right]\)
\(\displaystyle K_{m}^{(b)}(x, x') \to K^{(b)}(x, x') = E \left[ \sigma(a^t x) \sigma(a^t x') \right]\)
\(\displaystyle K^{(a)}(x, x') = \frac{(x x') E[b^2]}{2 \pi} (\pi - \theta(x, x))\)
\(\displaystyle K^{(b)}(x, x') = \frac{\Vert x \Vert \Vert x' \Vert E[\Vert a \Vert^2]}{2 \pi d} ((\pi - \theta(x, x')) \cos(\theta) + \sin \theta)\)
- Q
- When is this taylor approximation good?
If the Hessian has bounded eigenvalues. (Hessian Control)
- Analyze GD
\(\displaystyle \eta \to 0\) Gradient-flow
\(\displaystyle w(t+1) = w(t) - \eta \nabla_{w} L(w(t)) \implies \frac{w(t+1) - w(t)}{\eta} = - \nabla_{w} L(w(t))\)
\(\displaystyle \to \frac{dw(t)}{dt} = -\nabla_{w} L(w(t))\)
\(\displaystyle \frac{dw(t)}{dt} = -\nabla_{w} \hat{y}(w) (\hat{y}(w) - y)\)
\(\displaystyle
\begin{aligned}
\frac{d\hat{y}(w(t)}{dt} &= - \nabla_{w} \hat{y}(w(t))^2 \frac{dw(t)}{dt} \\
&= - \nabla_{w} \hat{y}(w(t))^2 \nabla_{w} \hat{y}(w) (\hat{y}(w) - y)\\
&\approx -K(w_0) (\hat{y}(w(t))-y)
\end{aligned}
\)
If we let \(\displaystyle u = \hat{y} - y\), then \(\displaystyle \frac{du}{dt} \approx -K(w_i) u\).
This ODE implies \(\displaystyle u(t) = u(0)\exp(-K(w_i)t)\).
In the over-parameterized case, \(\displaystyle K(w_0) \gt 0 \) (positive definite).
- SOTA NNs often outperform kernel methods (even based on NTKs)
Adversarial Robustness
Beginning of Lecture 8 (Sept. 24 2020)
In standard ERM, we have a dataset:
\(\displaystyle \{(x_i, y_i)\}_{i=1}^{n}\) where \(\displaystyle x_i \in \mathbb{R}^d\) and \(\displaystyle y_i \in [c]\)
We optimize \(\displaystyle \min_{\theta} E \left[ l(f_{\theta}(x), y) \right] = \frac{1}{n} \sum l(f_{\theta}(x_i), y_i) \).
- What is an adversarial example?
\(\displaystyle x'\) is an adversarial example for \(\displaystyle x\) under a model \(\displaystyle f_{\theta}()\) if
- \(\displaystyle f_{\theta}(x) \neq f_{\theta}(x')\) and
- \(\displaystyle f_{human}(x) = f_{human}(x)\)
One key challenge is that we don't have a precise definition of human perception.
Formulation
Threat Models: \(\displaystyle x' \in T(x, \epsilon)\)
Example: Lp model \(\displaystyle \{x' | \Vert x' - x \Vert_{lp} \leq \epsilon \}\)
Non-Lp threat models:
One problem with Lp models is that two identical images can have large L2 difference. For example, shifting or rotating an image.
An example of a non-Lp threat model is using Wasserstein difference.
Attacks
The goal is given \(\displaystyle x\) and \(\displaystyle f_{\theta}()\), we want to compute \(\displaystyle x'\) such that \(\displaystyle c* = f_{\theta}(x) \neq f_{\theta}(x')\).
- Targeted: Given a target label \(\displaystyle t \neq c^*\), \(\displaystyle f_{\theta}(x') = t\).
- Untargeted: \(\displaystyle c^*\) is not given
We mostly focus on targeted attacks.
- White-box: Adversary knows everything
- Black-box: Adversary has limited knowledge
We mostly focus on white-box attacks.
- Inference-time (evasion) attacks
- Training-time (poison) attacks
We focus on Inference-time attacks.
Attack Optimization:
\(\displaystyle \max_{\delta} l_{cls}(f_{\theta}(x'), y)\) such that \(\displaystyle \Vert x - x' \Vert \lt \epsilon\)
How to solve this optimization?
Fast Gradient Sign Method (FGSM)
For \(\displaystyle p=\infty\):
\(\displaystyle
\begin{aligned}
\delta_{FGSM} &= \max_{\Vert \delta \Vert \leq \epsilon} \lt \nabla l(f_{\theta}(x), y), \delta\gt \\
&= \epsilon sign(\nabla l(f_{\theta}(x), y))
\end{aligned}
\)
Pros:
- Fast because it is a one-step attack.
Projected Gradient Descent (PGD)
This is an iterative attack using gradient descent.
- Initalize \(\displaystyle x^(0) = x\)
- At each iteration, calculate \(\displaystyle \tilde{x}^{(t+1)} = x^{(t)} + \eta g^{(t)}\).
- Then project back into the ball \(\displaystyle x^{(t+1)} = \pi(\tilde{x}^{(t+1)}\).
- For \(\displaystyle l_{\infty}\), just do a element-wise clamp: \(\displaystyle x^{(t+1)} = clip(\tilde{x}^{(t+1)}, x - \epsilon, x + \epsilon)\)
In general, PGD > FGSM.
Alternative formulation
\(\displaystyle \min \Vert \delta \Vert\) such that \(\displaystyle f_{\theta}(x + \delta) = t \neq c^*\)
Lagrange dual form:
\(\displaystyle \min \Vert \delta \Vert - \lambda l_{cls}(f_{\theta}(x + \delta, y=c^*)\)
Adversarial Training
\(\displaystyle \min_{\theta} E \left[ \max_{x'} l_{cls}(f_{\theta}(x'), y) \right]\)
How to solve it?
- Inner max = attack problem (PGD)
- Outer max = gradient descent
Other heuristic/emperical defenses
Beginning of Lecture 9, Sept. 29 2020
ICLR 2018: 6-7 empirical defenses
Athalye et al (ICML 2018) show that obfuscated/masked gradients provide a false sense of security.
Such defenses can be easily broken using adaptive attacks. Obfuscated gradients provide shattered gradients (e.g. non-differentiable op) or stochastic gradients (e.g. randomized network).
- How to identify obfuscated or masked gradients?
Check the following:
- One step attack > iterative attack.
- Black-box attack > white-box attack.
- Unbounded attack (i.e. \(\displaystyle \rho\) can go to infinity) does not yield 100% success rate.
- Increasing attack budget doesn't increase the success rate.
If any of the above are true then your defense may be based on obfuscated or masked gradients.
- How to attack defenses using gradient masking?
- Defense based on adding a non-differentiable operator:
Example 1:
\(\displaystyle \hat{f}(x) = f(g(x))\) with g non-diff and non smooth.
In the attack, just use g(x)
Example 2:
Defense uses randomized classifier or stochastic gradients
Just take the expectation over the randomization.
Are adversarial examples inevitable?
Notations
\(\displaystyle S^{d-1} = \{x \in \mathbb{R} \mid \Vert x \Vert = 1\}\)
Let the geodesic distance be denoted by \(\displaystyle d_{g}\).
This is the length of the shortest path on the sphere.
On sphere: \(\displaystyle d_{\infty}(x, x') \leq d_{2}(x, x') \leq d_{g}(x, x')\).
Classification problem: \(\displaystyle \{1,..., C\} = [c]\) labels.
Each class has a density function \(\displaystyle \rho_{c}\) which is bounded.
Let \(\displaystyle U_c = \sup_{x} \rho_c(x)\) be the largest density we can get.
The \(\displaystyle \epsilon\)-expansion of A:
\(\displaystyle A(\epsilon, d) = \{x \mid d(x,z)\leq \epsilon \text{ for some } z \in A\}\).
Isoperimetric Inequality
Of all closed surfaces that encloses a unit volume, the sphere has the smallest surface.
Very intuitive but difficult to prove. (Osserman et al 1976)
- Lemma (Lerg & Pellegrino 1951, simplified by Talagrand 1995)
Consider a subset \(\displaystyle A \subset S^{d-1} \subset \mathbb{R}^n\) with normalized measure \(\displaystyle \mu_1(A) \geq 1/2\). Using the geodesic metric, the \(\displaystyle \epsilon\)-expansion \(\displaystyle A(\epsilon)\) is at least as large as the \(\displaystyle \epsilon\)-expansion of a half sphere.
- Lemma (Milman & Schechtman 1986)
\(\displaystyle A(\epsilon) \geq 1 - (\frac{\pi}{8})^{1/2} \exp(-\frac{d-1}{2} \epsilon^2)\)
As d goes to infinity, the right hand side goes to 1.
In a high-dimensional space, an epsilon expansion will cover almost the entire area.
Theorem
c-class classification
\(\displaystyle \rho_c, u_c\)
\(\displaystyle v_c=\delta_{n-1} * u_c\) is the max density relative to uniform density.
\(\displaystyle f_c = \mu_1 \{x \mid C(x)=c\}\) is the area where the classifier \(\displaystyle C\) classifies as class c.
Pick a class such that \(\displaystyle f_c \leq \frac{1}{2}\).
Sample a random point x from the true density \(\displaystyle \rho_c\).
With high probability, either:
- x is misclassified or,
- x has an \(\displaystyle \epsilon\)-close adversarial example.
One of these will happen with probability \(\displaystyle 1-v_c (\frac{\pi}{8})^{1/2} \exp^{- ((d-1)/2) \epsilon^2}\)
Proof:
Consider the region with the correct classification: \(\displaystyle R=\{x \mid c(x)=c\).
Here \(\displaystyle u(R) = f_c \leq 1/2\).
Consider the compliment \(\displaystyle R^c\).
The area of the complement is \(\displaystyle u_1(R^c) \geq \frac{1}{2}\).
The area of the epsilon expansion is \(\displaystyle u_1(R^c(\epsilon)) \geq 1 - (\pi/8)^{1/2} \exp(-\frac{d-1}{2}\epsilon^2)\). Thus the safe zone is very small in high dimension.
Cubes
Geometric isoparametric inequalities do not exist for cubes. However, algebraic inequalities exist.
- Lemma
\(\displaystyle A \subset [0, 1]^d\) with \(\displaystyle vol(A) \geq \frac{1}{2}\)
\(\displaystyle vol(A(\epsilon g d p)) \geq 1 - \frac{\exp(-2 \pi d^{1-(2/p^2)\epsilon^2})}{2 \pi \epsilon d^{1/2 - 1/p^2}}\)
For l2 p>=2, \(\displaystyle p \geq 2\), \(\displaystyle vol(A(\epsilon g d p)) \geq 1 - \frac{\exp(-2 \pi \epsilon^2)}{2 \pi \epsilon}\)
For p=2, the diameter of the hypercube is \(\displaystyle O(\sqrt{d})\) so we should use \(\displaystyle \epsilon \approx O(\sqrt{d})\).
For p=infinity, the diameter of the cube is 1 so we should pick a constant \(\displaystyle \epsilon\).
This shows if you pick a random sample, there is a high probability of it being misclassified or there being an adversarial example within epsilon.
Are adversarial examples inevitable in practice?
This is an ill-posed question.
It depends on the data distribution, threat model, and hypothesis class.
Provable Defenses
There are 3 types of Lp defenses:
- Curvature-based defenses
- IBP and Convex defenses
- Randomzied smoothing
For Non-Lp
- Patch Threat
- Sparse Threat
- Wasserstein Threat
Randomized Smoothing
A smoothed classifier: \(\displaystyle \bar{f}(x) = E_{\epsilon}[f(x+\epsilon)]\). The idea is that the decision boundary becomes smoother.
Gaussian Smoothing for L2 attacks:
- Theorem (Cohen et al., 2019)
No adversarial example exists within the radius:
\(\displaystyle \frac{\sigma}{2}\left(\Phi^{-1}(p_1(x))-\Phi^{-1}(p_2(x))\right)\)
The proof is based on Neyman & Pearson lemma.
- Theorem (Levine, Singla, F2019, Salman et al 2019)
\(\displaystyle \Phi^{-1}(\bar{f}(x))\) is Lipschitz with constant \(\displaystyle 1/\sigma\)
The worst g is a stepwise function. Then \(\displaystyle \Phi^{-1}(\bar{g})\) is a linear function.
For L2 attacks, you can use Gaussian noise. For L1 attacks, you can use Laplace noise.
- Theorem (KLGF, ICML 2020)
Using any symmetric i.i.d. smoothing, \(\displaystyle r_{p}^* \leq \frac{\sigma}{2 \sqrt{2} d^{1/2 - 1/p}}\left(\frac{1}{\sqrt{1-p_1(x)}} + \frac{1}{\sqrt{p_2(x)}}\right)\)
If we use Gaussian smoothing against Lp attacks, we get:
\(\displaystyle r_p = \frac{\sigma}{2d^{1/2 - 1/p}}\left( \Sigma^{-1}(p_1(x)) - \Sigma^{-1}(p_2(x)) \right)\)
This shows that Gaussian smoothing is optimal (up to a constant) within i.i.d. smoothing distributions against Lp attacks.
Sparse Threat
Here the adversary can change up to \(\displaystyle \rho\) pixels in the image.
The idea is to classify each example based on only k random pixels in the image. This is performed several times and the a voting scheme determines the final label.
- Theorem (Levine, F. AAAI 2020)
For inputs \(\displaystyle x\) and \(\displaystyle x'\) with \(\displaystyle \Vert x - x' \Vert_{l_0} \leq \rho\), for all i \(\displaystyle \vert p_i(x) - p_i(x')\vert \leq \delta\) where \(\displaystyle \delta = 1 - \frac{\binom{d-\rho}{k}}{\binom{d}{k}}\).
Robustness vs Accuracy Trade-off:
Increasing \(\displaystyle k\) boosts classification accuracy but also increases \(\displaystyle \Delta\).
Relationship between Threat Models
Use a neural perceptual threat model to approximate the true perceptual distance.
Use LPIPS as \(\displaystyle d_{neural}(x, x') = \Vert \phi(x) - \phi(x') \Vert\) where \(\displaystyle \phi\) are normalized feature maps.
Our attack optimization is now:
\(\displaystyle
\begin{aligned}
\max_{x'} &l_{cls}(f(x'), y)\\
& d_{neural}(x, x') \leq \rho
\end{aligned}
\)
From this, we get Perceptual Projected Gradient Descent (PPGD) and Lagrangian Perceptual Attacks (LPA).
We also get Perceptual Adversarial Training (PAT).
Poisoning Attacks and Defenses
Another type of adversarial robustness.
So far, we train on training data using SGD and do adversarial attacks at inference time.
However, deep learning models require a large amount of training data which makes it hard to manually verify or trust training samples.
In this case, an adversary can do data poisoning by perturbing some of the training samples.
- Question
- What is the goal of data poisoning?
- To reduce the test time accuracy?
- Simple to mitigate by looking at the performance for validation set.
- Targeted misclassification: to cause one or more target samples to be misclassified as another class.
- This is what we focus on
Given clean/base images: \(\displaystyle \{(x_i, y_i)\}_{i=1}^{n}\), create poison images \(\displaystyle \{(x_i^{(P)},y_i^{(P)}\}_{i=1}^{J}\).
Our new training set is: \(\displaystyle \{(x_i, y_i)\}_{i=1}^{n} \cup \{(x_i^{(P)},y_i^{(P)}\}_{i=1}^{J}\).
We train using SGD on some model \(\displaystyle f\).
The goal is to make \(\displaystyle f(x_t)\) produce the wrong label.
Naive attack
\(\displaystyle x_t\) is a cat. Our goal is that \(\displaystyle f(x_t)\) is dog.
One way is to add multiple examples of \(\displaystyle x_t\) with the wrong label, dog.
For a sufficiently large model, it will predict a dog image.
This is called flooding the training set.
This is not too concerning because a simple filtering or outlier detection can identify poison samples.
Two types of attacks
- backdoor attacks
- triggerless attacks
Backdoor attacks
The idea is too add a trigger or watermark to the image to make it misclassify it.
Gu et al (2017) [7] randomly select a small portion of training set, apply a backdoor trigger, and change the label to the target label.
However this is not a clean attack because you need to change the labels.
Turnet et al. craft clean-label backdoor attacks.
Here they take examples \(\displaystyle x_j^{(b)}\) (e.g. airplane) and apply an adversarial perturbation to get \(\displaystyle \tilde{x}_j^{(b)}\).
The adversarial perturbation is obtained by training a network \(\displaystyle g\).
By the transferability of adversarial attacks, a new network \(\displaystyle f\) is likely to output a wrong label.
Then they add a trigger to the image.
Pros: You can use the trigger to poison several examples.
Cons: There is a trigger.
Triggerless poison attacks
Shafahi et al introduce feature collisions.
Suppose f is the feature layer and g is a pretrained network.
Suppose x_t is a cat and g classified cats and airplanes.
The idea is to apply adversarial perturbation to some base image to be close to the target in the feature space.
If we train the model on the poisoned samples, the decision boundary is going to fold.
\(\displaystyle
x_j^{(p)} = \operatorname{argmax}_{x} \Vert g(x) - g(x_t) \Vert_{l2}^{2} + \beta \Vert x - x_j^{(b)} \Vert _{l2}^2
\)
- Do these attacks actually work?
Schwarz Schild et al. test on multiple datasets and find that these attack do not really work.
The attacks are heavily dependent on the particular setup.
- Feature Collision attack: they assume g is trained on adam but the success rate is bad for SGD.
- Data augmentation: Success rates falls for different model.
- For black-box attacks, success rate reduces
- Success rate also depends on the size of the dataset.
Provable defenses against general poison attacks
Levine and Feizi (2020)
Consider a general poisoning attack where the attacker can insert or remove samples from the training set.
We measure the attack magnitude by the symmetric difference between the clean and poisoned sets.
Symmetric difference is defined as \(\displaystyle A \ominus B = (A \setminus B) \cup (B \setminus A)\).
Last lecture, we had provable defenses against sparse inference time attacks using randomized ablation.
Deep Partition Aggregation (DPA):
- Partition the training set into \(\displaystyle k\) partitions.
- Use a hash function \(\displaystyle h\) to deterministically define partition assignments for samples. The hash should only depend on \(\displaystyle x\) and not the labels \(\displaystyle y\).
- Train a classifier for each partition: \(\displaystyle f_1,...,f_k\).
- At test time, run \(\displaystyle x_t\) through every classifier and take the majority class.
\(\displaystyle K_1\) be the base classifier returning the majority class \(\displaystyle C\).
\(\displaystyle K_2\) be the runner up class \(\displaystyle C'\).
The gap \(\displaystyle \Delta = K_1 - K_2\).
To change the plurality C to C', the adversary needs to change the output of at least \(\displaystyle \Delta/2\) base classifiers.
This is probably robust against any insertion/deletion \(\displaystyle \leq \Delta/2\).
Both DPA and SS-DPA (semi-supervised DPA) are state-of-the-art against label flipping attacks.
Variational Autoencoders (VAE)
Deep generative models:
Given training data \(\displaystyle \{x_i\}_{i=1}^{n}\).
The goal is to generate realistic fake samples.
Given a good generative model, we can do denoising, inpainting, domain transfer, etc.
Probabilistic Model: Suppose our dataset is \(\displaystyle \{x_i\}_{1}^{n}\) with \(\displaystyle x_i \in \mathbb{R}^d\)
- Generate latent variables \(\displaystyle z_1,...,z_n \in \mathbb{R}^r\) where \(\displaystyle r \lt \lt d\).
- Assume \(\displaystyle X=x_i | Z = z_i \sim N \left( g_{theta}(z_i), \sigma^2 I \right)\).
- Here \(\displaystyle g_\theta\) is called the generator or decoder function.
Q: How can we pick good model parameters \(\displaystyle \theta\)?
Using maximum likelihood:
\(\displaystyle \begin{align*} \max_{\theta} P(\{x_i\}; \theta) &= \prod P(x_i; \theta)\\ &= \max_{\theta} \sum_{i=1}^{n} \log P_{\theta}(x_i)\\ &= \max_{\theta} \sum_{i=1}^{n} \log \left( \int_{z} P(z) P(x_i|z) dz \right)\\ \end{align*} \)
This is hard to compute.
Instead we calculate a lower bound and maximize the lower bound:
\(\displaystyle \max_{\theta} l(\theta) \geq \max_{\theta, \phi} J(\theta, \phi)\)
ELBO / Variational lower bound
\(\displaystyle \begin{aligned} &P(x_i | z) = \frac{P(z | x_i) P(x_i)}{P(z)}\\ \implies& \log P(x_i | z) + \log P(z) = \log P(z | x_i) + \log P(x_i)\\ \implies& E_z[\log P(x_i)] = E[ \log P(x_i | z) + \log P(z) - \log P(z | x_i)] \\ \implies& \log P(x_i) = E_{z \sim q_i}[\log P_{\theta}(x_i | z)] + E[\log P(z)] - E[\log P(z|x_i)] + (E[\log q_i(z)] - E[\log q_i(z)])\\ \implies& \log P(x_i) = E_{z \sim q_i}[\log P_{\theta}(x_i | z)] + (E_q[\log q_i(z)]- E_q[\log P(z|x_i)]) - (E_q[\log q_i(z) - E_q[\log P(z)]])\\ \implies& \log P(x_i) = E_{z \sim q_i} \left[\log P_{\theta}(x_i | z) \right] + KL \left(q_i \Vert P(z|x_i) \right) - KL \left(q_i \Vert P(z) \right)\\ \end{aligned} \)
The second term is hard to compute so we ignore it. It is a positive term.
Thus:
\(\displaystyle \log P(x_i) \geq E_{z \sim q_i} \left[\log P_{\theta}(x_i | z) \right] - KL \left(q_i \Vert P(z) \right)\)
Optimization:
\(\displaystyle \max_{\theta, \phi} \sum_{i=1}^{n} E_{z \sim q} \left[\log P_{\theta}(x_i | z) \right] - KL \left(q_i \Vert P(z) \right)\)
\(\displaystyle q(z|x) \sim N\left( f_{\phi}(x), \sigma^2 I \right)\)
Here, \(\displaystyle f_{\phi}(x)\) is called the encoder.
The claim is that \(\displaystyle KL \left(q_i \Vert P(z) \right)\) is easier to compute:
\(\displaystyle
\begin{align*}
&\max_{\theta, \phi} \sum_{i=1}^{n} E_{z \sim q} \left[\log P_{\theta}(x_i | z) \right] - KL \left(q_i \Vert P(z) \right)\\
=&\max_{\theta, \phi} \sum_{i=1}^{n} E_{z \sim q} \left[ \log \exp(-\Vert x_i - g_{\theta}(z) \Vert^2 /(2\sigma^2)) - \log \exp(-\Vert z - f_{\phi}(z) \Vert^2 /(2\sigma^2)) \right]\\
=&\max_{\theta, \phi} \sum_{i=1}^{n} E_{z \sim q} \left[ -\Vert x_i - g_{\theta}(z) \Vert^2 /(2\sigma^2) + \Vert z - f_{\phi}(z) \Vert^2 /(2\sigma^2) \right]\\
\end{align*}
\)
We use SGD to optimize \(\displaystyle \theta, \phi\).
Using the reparameterization trick, \(\displaystyle z = \mu + \Sigma^{1/2}\epsilon\) for \(\displaystyle \epsilon \sim N(0, I)\).
- ELBO
\(\displaystyle \max_{\theta, \phi} E_{z \sim q}[\log P(x|z)] - KL(q(z|x) \Vert P(z))\)
Issue: Posterior collapse.
In practice, sometimes the posterior \(\displaystyle q\) does not depend on x: \(\displaystyle q(z|x) \approx q(z)\).
β-VAE
VAEs have many design choices:
- Prior distribution \(\displaystyle P(z)\) chosen to be normal.
- Posterior distribution \(\displaystyle q(z|x)\) chosen to be \(\displaystyle N(f(x), \sigma^2 I)\).
However this often leads to blurry images.
One way to address this is to increase the expressiveness of the prior and posterior distributions.
This leads to Hierarchical VAEs.
The idea is that latent variables are partitioned to disjoint groups:
\(\displaystyle z = \{z_1, ..., z_L\}\)
\(\displaystyle P(z) = \prod_{l}P(z_l | z_{\lt l})\)
\(\displaystyle q(z|x) = \prod_{l}q(z_l | z_{\lt l}, x)\)
Vandet et al. create NVAE which is Hierarchical VAE + some tricks.
VQ-VAE (Vector quantized VAE) perform quantization of the latent space.
The quantization is non differentiable but they can copy the gradients.
Generative Adversarial Networks (GANs)
Given data \(\displaystyle \{y_1,...,y_n\}\).
The goal of the generator is to take random noise \(\displaystyle \{x_i,...,x_n\}\) and generate fake data \(\displaystyle \{\hat{y}_1,...,\hat{y}_n\}\).
Then there is a discriminator which takes in \(\displaystyle \{y_i\}\) and \(\displaystyle \{\hat{y}_i\}\) and guide the generator.
In practice, both use deep neural networks.
The optimization is \(\displaystyle \min_{G} \max_{D} f(G, D)\).
GAN training is challenging.
Oftentimes, there are convergence issues.
There can also be mode collapsing issues.
Generalization can be poor and performance evaluation is subjective.
A common approach for training GANs is using alternating gradient descent.
However, this usually does not converge to \(\displaystyle G^*\).
Reducing unsupervised to supervised
- Formulating GANs
Given \(\displaystyle \{y_i\}\) and \(\displaystyle \{x_i\}\).
We need to find a generator \(\displaystyle G\) s.t. \(\displaystyle G(X) \stackrel{\text{dist}}{\approx} Y\).
Given some data \(\displaystyle \{y_i\}\), generate some randomness \(\displaystyle \{x_i\}\).
Create a coupling \(\displaystyle \pi()\) to create paired examples \(\displaystyle \{(x_{\pi(i)}, y_i)\}\).
Then we have:
\(\displaystyle \min_{\pi} \min_{G} \frac{1}{n} \sum_{i=1}^{n} l(\mathbf{y}_i, G(\mathbf{x}_{\pi(i)}))\)
We can replace the coupling with a joint distribution:
\(\displaystyle \min_{\mathbb{P}_{X, Y}} \min_{G} \frac{1}{n} E_{\mathbb{P}_{X,Y}}[ l(\mathbf{y}_i, G(\mathbf{x}_{\pi(i)}))]\).
By switching the min and substituting \(\displaystyle \hat{Y} = G(X)\):
\(\displaystyle \min_{G} \min_{\mathbb{P}} E_{\mathbb{P}_{X,Y}}[l(Y, \hat{Y})]\).
The inner minimization is the optimal transport distance.
Optimal Transport (Earth-Mover)
Non-parametric distances between probability measures.
This is well-defined.
Cost of transporting yellow to red points:
\(\displaystyle \min_{\pi} \frac{1}{n} \sum_{i=1}^{n} l(y_i, \hat{y}_{\pi(i)})\).
If using l2, then \(\displaystyle dist(P_{Y},P_{\hat{Y}}) = W(P_{Y}, P_{\hat{Y}})\).
- Optimization
The primal is \(\displaystyle dist(P_Y, Y_{\hat{Y}}) = \min E[l(Y, \hat{Y})]\).
- WGAN Formulation
The dual of \(\displaystyle \min_{G} W_1(P_Y, P_{\hat{Y}})\) is \(\displaystyle \min_{G} \max_{D} \left[ E[D(Y)] - E[D(\hat{Y})] \right]\).
The lipschitz of the discriminator can be enforced by weight clipping.
How to evaluate GANs?
- Inception Score
Use a pre-trained network (Inception-v3) to map a generated image to its probabilities.
\(\displaystyle IS(G) = \exp \left( E_{x \sim P_{\hat{X}}} KL( p(y|x) \Vert p(y) ) \right)\)
Mutual Information interpretation:
\(\displaystyle \log(IS(G)) = I(G(Z);y) = H(y) - H(y|G(z))\)
- The first term \(\displaystyle H(y)\) represents diverse labels.
- The second score represents high confidence.
IS is misleading if it only generates one image per class.
- FID Score
Use a pre-trained network (Inception) to extract features from an intermediate layer.
Then model the data distribution using multivariate Gaussian with mean \(\displaystyle \mu\) and covariance \(\displaystyle \Sigma\).
FID is Frechet Inception Distance.
\(\displaystyle FID(x, y) = \Vert \mu_{x} - \mu_{g} \Vert_2^2 + Tr(\Sigma_{x} + \Sigma_g - 2(\Sigma_x \Sigma_g)^{1/2})\)
A Statistical Approach to GANs
GANs do not have explicit probability models.
This is in contrast to maximum-likelihood models like VAEs.
GANs focus on minimizing distance between distributions.
This yields high-quality samples but inability to sample likelihoods.
VAEs maximize lower bound on likelihood. However, you get blurry samples.
The key idea is to have an explicit model for the data: \(\displaystyle f_{Y}(y|X=x) ~ exp(-l(y, G(x))/\lambda)\)
- Theorem (BHCF 2019)
...
Entropic GANs meat VAEs.
Distributionally Robust Wasserstein
Robust Wasserstein: \(\displaystyle \begin{aligned} \min_{P_{\tilde{X}}, P_{\tilde{Y}}} \end{aligned} \)
Min-max Optimization
Beginning of Lecture 14 (Oct. 15, 2020) \(\displaystyle \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\VCdim}{VCdim} \DeclareMathOperator{\sign}{sign} \DeclareMathOperator{\rank}{rank} \DeclareMathOperator{\argmin}{argmin} \DeclareMathOperator{\argmax}{argmax} \)
- Problem
\(\displaystyle \min_{x \in X} \max_{y \in Y} f(x,y)\).
- This is a zero-sum game.
- Assume \(\displaystyle f\) is smooth and differentiable.
- Goal
Find \(\displaystyle (x^*, y^*)\) which is a global solution, saddle point, or equilibrium
- \(\displaystyle y^* \in \argmax f(x^*,y)\)
- \(\displaystyle x^* \in \argmin f(x, y^*)\)
We know: \(\displaystyle f(x^*,y) \leq f(x^*, y^*) \leq f(x, y^*)\)
Simultaneous Gradient Descent (GDA)
\(\displaystyle \begin{cases} x_{t+1} = x_t - \eta \nabla_{x} f(x_t, y_t)\\ y_{t+1} = y_t + \eta \nabla_{y} f(x_t, y_t) \end{cases} \)
- Notes
- \(\displaystyle x, y \in \mathbb{R}^d\)
- In the constrained case, we need to project back onto \(\displaystyle S\).
Define \(\displaystyle \theta = [x, y]\).
Then we can write the above update equation as \(\displaystyle \theta_{t+1} = \theta_{t} + \eta \overrightarrow{g}(\theta_t)\) where
\(\displaystyle \overrightarrow{g}(\theta_t) =
\begin{bmatrix}
- \nabla_x f(x_t, y_t)\\
\nabla_y f(x_t, y_t)
\end{bmatrix}
\)
Or in other words, \(\displaystyle \theta_{t+1} = F(\theta_t)\).
We want \(\displaystyle F\) to lead to \(\displaystyle \theta^*\) until \(\displaystyle \theta^* = F(\theta^*)\).
Here, \(\displaystyle \theta^*\) is a fixed point of \(\displaystyle F\).
Convex-concave min-max
The min-max theorem by [Von Neumann (1928)].
- Suppose \(\displaystyle X,Y\) be compact/convex.
- Suppose \(\displaystyle f\) is continuous and convex-concave.
Then:
- \(\displaystyle \min_{x \in X} \max_{y \in Y} f(x,y) = \max_{y \in Y} \min_{x \in X} f(x,y)\)
- min-max optimal point is unique if f is strictly convex-concave otherwise a convex-set of solutions exists.
- Notes
- If \(\displaystyle f\) is non-convex concave, it doesn't hold.
- bilinear core: \(\displaystyle f(x,y) = x^t A y + b^t x + c^t y\)
[Von Neumann-Dantzig 1947] show that there is a strong connection between the min-max theorem and strong \(\displaystyle L_p\) duality.
[Frennd & Schapive 199] show the convergence of sim GDA in an average sense:
Assume:
- f-> convex in x/concave in y
- S-> convex/compact/bounded
- \(\displaystyle \eta \approx \frac{1}{\sqrt{T}}\)
Then for Sim GDA: \(\displaystyle f(\bar{x}, \bar{y}) \to f(x^*, y^*)\) with order \(\displaystyle O(1/\sqrt{T})\)
No guarantees exist for the last iteration.
Optimistic GDA (OGDA)
Gradient descent with negative momentum:
\(\displaystyle x_{t+1} = x_t - \eta \nabla f(x_t) + \frac{\eta}{2} \nabla f(x_{t-1})\)
This technique by [Popov 1980] helps the convergence stability of GD.
- OGDA
\(\displaystyle \begin{cases} x_{t+1} = x_t - \eta \nabla_x f(x_t, y_t) + \frac{\eta}{2} \nabla_x f(x_{t-1},y_{t-1})\\ y_{t+1} = y_t + \eta \nabla_y f(x_t, y_t) - \frac{\eta}{2} \nabla_y f(x_{t-1},y_{t-1}) \end{cases} \)
OGDA has last iter convergence and linear rates for unconstrained bilinear min-max.
Nonconvex-nonconcave min-max opt
The goal is to find a local saddle point.
Stability
If we drift away from \(\displaystyle (x^*,y^*)\) then the optimization is unstable.
If we remain close, the optimization is stable even if we never converge.
- Asymptotic Stability
If dynamics start close enough to \(\displaystyle \theta^*\) it remains close.
If dynamics converges to \(\displaystyle \theta^*\), it is locally asymptotically stable.
Recall \(\displaystyle \theta_{t+1} = F(\theta_t) = \theta_t + \eta \overrightarrow{g}(\theta_t)\).
Jacobian of f: \(\displaystyle J(\theta) = I + \eta H(\theta)\). where the Hessian is \(\displaystyle H(\theta) = \begin{pmatrix} - \nabla_{xx}^2 f & -\nabla_{xy}^2 f\\ \nabla_{xy}^2 f & \nabla_{yy}^2 f\\ \end{pmatrix} \)
(Linear) stability: a fixed point \(\displaystyle \theta^*\) is stable if
\(\displaystyle | \lambda_{\max}(J(\theta^*)) | = \rho(J(\theta^*)) \leq 1\).
Lemma: If linearly stable but \(\displaystyle \rho(J(\theta^*)) \lt 1\) then asymptotic stability.
Strongly local min-max
Definition:
\(\displaystyle
\begin{cases}
\lambda_{min}(\nabla^2_{xx} f) \gt 0\\
\lambda_{max}(\nabla^2_{yy} f) \lt 0
\end{cases}
\)
Simultaneous GDA:
\(\displaystyle H =
\begin{pmatrix}
- \nabla_{xx}^2 f & -\nabla_{xy}^2 f\\
\nabla_{xy}^2 f & \nabla_{yy}^2 f\\
\end{pmatrix}
\)
Consider \(\displaystyle \theta^*\) is a local min-max. Then both of the diagonal matrices (\(\displaystyle -\nabla^2_{xx}\) and \(\displaystyle \nabla^2_{yy} f\)) will be negative semi definite.
Lemma:
Eigenvalues of the hessian matrix will not have a positive real part: \(\displaystyle Re(\lambda(H)) \lt 0\).
Why?
\(\displaystyle
\begin{pmatrix}
A & B\\
-B^T & C
\end{pmatrix}
\begin{pmatrix}
v \\ u
\end{pmatrix}
=
\lambda
\begin{pmatrix}
v \\ u
\end{pmatrix}
\)
Summing up both results in:
\(\displaystyle
\begin{aligned}
&(v^H A v + u^H C u) + (v^H B u - u^H B^T v) = \lambda (\Vert v \Vert^2 + \Vert u \Vert^2)\\
\implies &Re(v^H A v + u^H C u) = Re(\lambda)(\Vert v \Vert^2 + \Vert u \Vert^2) \lt 0\\
\implies &Re(\lambda) \lt 0
\end{aligned}
\)
For asymptotic stability, we need \(\displaystyle | \lambda_{\max} (J) | \lt 1\).
\(\displaystyle J = I + \eta H\) with lr \(\displaystyle \eta \gt 0\)
- Lemma
If H has eigenvalue with negative real parts then eigenvalues of J lie in a unit ball iff \(\displaystyle \eta \lt \frac{1}{|Re(\lambda)} \frac{2}{1+ (Im(\lambda)/Re(\lambda))^2}\) for all \(\displaystyle \lambda\).
The convergence rate of Sim GDA is proportional to the spectral radius \(\displaystyle O(\rho(J)^t)\).
Thus we want the spectral radius to be small (e.g. 1/2) for a fast convergence rate.
Suppose we have a really large negative real part in the eigenvalue. Then \(\displaystyle \eta\) will need to be really small which we don't want. Similarly if \(\displaystyle Im(\lambda)/Re(\lambda)\) is large then we will have slow convergence.
Regularized GDA
\(\displaystyle \theta_{t+1} = \theta_t + \eta R(\theta_t) G(\theta_t)\)
- \(\displaystyle R(\theta)\) is chosen to not change the fixed point of the original problewm.
- Suppose \(\displaystyle R(\theta)\) is invertible. \(\displaystyle \theta^*\) is a fixed point iff \(\displaystyle g(\theta^*) = 0\).
Proof:
(->) If \(\displaystyle \theta^*\lt /math. is a fixed point the \lt math\gt 0 = \eta R(\theta^*) g(\theta^*) \implies g(\theta^*) = 0\).
(<-) If \(\displaystyle g(\theta^*)=0\), we want to show \(\displaystyle \theta^*\) is a fixed point.
If \(\displaystyle g(\theta^*)=0\) then \(\displaystyle \tilde{J}(\theta^*) = I + \eta R(\theta^*) H(\theta^*) + 0\).
\(\displaystyle R(\theta) = I - \gamma H^T\)
\(\displaystyle R(\theta) H(\theta) = (I-\gamma H^T)H = H - \gamma H^T H\)
\(\displaystyle J = I - \eta H - \eta \gamma H^T H\)
Thus this regularization pushes the real parts of the eigenvalues to be more negative so that the training will be more stable.
This reduces \(\displaystyle Im(\lambda)/Re(\lambda)\) but may not necessarily help because it increases \(\displaystyle Re(\lambda)\).
Approximate Local minmax
Under continuous and differentiable assumptions, the space of fixed-points is guaranteed to be non-empty (by Brouwev's Fixed Point thm) however the set of local min-max can be empty.
[Dskalakis & Penges 2018, Adolphs et al 2018]
In an unconstrained case, the strong local min-max set is a subset of stabled fixed points of GDA which is a subset of stable points of OGDA.
- Definition
\(\displaystyle (x^*, y^*)\) is an \(\displaystyle (\epsilon, \delta)\) approximate local min-max if:
\(\displaystyle f(x^*, y) - \epsilon \leq f(x^*, y^*) \leq f(x, y^*) + \epsilon\)
\(\displaystyle \forall (x,y) \in B_{\delta}(x^*, y^*)\)
Suppose f is a G-lipschitz and L-smooth.
For \(\displaystyle \delta \lt \epsilon/G\), every point is a local min-max.
For \(\displaystyle \delta \gt \sqrt{2\epsilon/L}\), the local min-max may not exist and np-hard to compute.
For the region in between, the local min max is guaranteed to exist. The compute is PPAD (super polynomial) and not np-hard.
- So what?
For ERM non-convex minimization, we us GD to solve. Over-parameterization helped us in terms of global convergence.
Would over-parameterization help in solving non-convex concave min-max?
Yes. An ICLR 2021 paper by anonymous authors Understanding the role of over-parameterization in GANs.
- Theorem
Consider a WGAN problem.
Suppose the generator is one-hidden layer and the discriminator is linear.
\(\displaystyle \min_{G} \max_{D} f(G,D)\) is non-convex concave optimization.
If the generator is sufficiently over-parameterized then Sim GDA converges to a global min-max solution.
Flow-based Generative Models
Lecture 16 (October 22, 2020)
Suppose we have a dataset \(\displaystyle \{x_1,..., x_n\} \subset \mathbb{R}^d\).
Our probabilistic model is:
\(\displaystyle z \sim N(0,I)\) and \(\displaystyle x=g_{\theta}(z)\) where g is bijective and invertible.
We assume \(\displaystyle f\) is a differentiable function.
Generation or sampling goes from \(\displaystyle z\) to \(\displaystyle x\).
Inference goes from \(\displaystyle x\) to \(\displaystyle z\).
Change of variables in 1d: \(\displaystyle P(z)dz = P(x)dx \implies P(x) = P(z) \frac{dz}{dx}\).
In high-dim: \(\displaystyle P(x) = P(z) | det(\frac{dz}{dx}) |\).
- Maximum Likelihood
\(\displaystyle P_{\theta}(x) = P(z) | det(\frac{dz}{dx})|\).
\(\displaystyle
\begin{aligned}
\max_{\theta} \frac{1}{n} \sum_{i=1}^{n} \log P_{\theta}(x_i) \\
= \min_{\theta} \frac{1}{n} \sum_{i=1}^{n} \left[ -\log P_{\theta}(x_i) \right]\\
= \min_{\theta} \frac{-1}{n} \sum_{i=1}^{n} \left[ \log P(z_i) + \log | det(\frac{dz}{dx})| \right]
\end{aligned}
\)
- Issues
- How to design a bijective function?
- \(\displaystyle det(J)\) computation can be very expensive.
- Idea
- Come up with J (i.e. f/g mappings) such that det(J) is easy to compute.
If \(\displaystyle J\) is a diagonal matrix then \(\displaystyle det(J) = \prod_i J_{ii}\).
An \(\displaystyle f\) function which is element-wise would have a diagonal jacobian. This is not very expressive.
Upper-triangular Jacobian
RealNVP by [Dint et al] considers an upper-triangular matrix.
In this case, the determinant is still the diagonal.
What does f/g look like?
\(\displaystyle
\begin{cases}
z_1 = x_1\\
z_2 = s_\theta \cdot x_2 + t_\theta
\end{cases}
\)
Now our jacobian is:
\(\displaystyle
J = \begin{pmatrix}
I & 0\\
\frac{dz_2}{dx_1} & diag(S_\theta)
\end{pmatrix}
\)
and \(\displaystyle det(J) = \prod (S_\theta)_i\).
Is this expressive enough? No.
Composition of transformations
\(\displaystyle f = f_1 \circ f_2 \circ ... \circ f_k\)
A sequence of invertible transformations is called normalizing flows.
Here, we have the following properties
- \(\displaystyle (f_1 \circ f_2)^{-1} = f_2^{-1} \circ f_1^{-1}\)
- \(\displaystyle \nabla(f_2 \circ f_1)(x) = \nabla f_2(f_1(x)) \nabla f_1(x)\)
- \(\displaystyle det(J_1 J_2) = det(J_1) det(J_2)\)
RealNVP uses two types of partitioning
- Checkerboard
- Channel partitioning
In Glow [Kingmen et al], they use invertible 1x1 convolution which is equivalent to matrix multiplication.
Use \(\displaystyle W = P L (U+diag(s))\) and \(\displaystyle | det(W)| = sum(\log |S|)\)
Dequantization
Fitting a density function to discrete data can have crazy peaks.
For dequantization, add a uniform to the data to get a more stable density function.
\(\displaystyle \begin{aligned} \log \int p(x_i +\delta) p(\delta)ds &= \log E_\delta [\log p(x_i + \delta)]\\ &\geq E_{\delta}[\log p(x_i + \delta)]\\ &\approx \log p(x_i + \delta) \end{aligned} \)
- We have exact likelihood estimations.
- We can use out-of-distribution anomaly detection.
However in practice after training on CIFAR, the liklihood of MNIST is higher.
This behavior is not specific to flow-based models.
Suppose \(\displaystyle P_{\theta}\) is \(\displaystyle N(0, I_d)\).
Our typical example has \(\displaystyle \Vert x_i \Vert^2 = O(d)\).
Consider \(\displaystyle x^{test} = 0\) then \(\displaystyle P_{\theta}(x^{test}) \gt P_{\theta}(x_1)\).
Domain Adaptation
So far, we have a training set \(\displaystyle \{(x_i^{(train)}, y_i^{(train)})\}\) from distribution \(\displaystyle Q_{X,Y}\).
We learn optimal parameters \(\displaystyle \theta^*\) via ERM.
Then at test time, our test samples come from the same distribution \(\displaystyle Q_{X,Y}\).
However in practice, the training distribution can be different from the test distribution.
The training distribution is the source domain. The test distribution is the target domain.
- Examples
Q may be synthetic samples and P may be real samples.
Q contains samples with white background but P has samples with real backgrounds.
In training:
For the source domain, we have labeled samples \(\displaystyle \{(x_i^S, y_i^S)\}_{i=1}^{m_S} \sim Q_{X,Y}\).
For the target domain, we only have unlabeled samples \(\displaystyle \{x_i^t\} \sim P_{X}\).
This is unsupervised domain adaptation.
In semi-supervised domain adaptation, your target samples are mostly unlabeled but contain a few labeled samples.
If no target samples are available during training, the scenario is called domain generalization or out-of-distribution generalization.
Unsupervised domain adaptation
Given \(\displaystyle m_s = m_t = m\).
- m labeled samples from source domain Q
- m unlabeled samples from target P
- This problem is ill-defined
- Practical assumptions.
- Covariate shifts: P and Q satisfy the covariate shift assumption if the conditional label dist doesn't change between source and target.
- I.e. \(\displaystyle P(y|x) = Q(y|x)\)
- Similarity of source and target marginal distributions.
- If I had labeled target samples, the joint error (target + source samples) should be small.
[Ben-David et al.] consider binary classification.
- H-divergence
\(\displaystyle 2 \sup_{h \in H}|Pr_{x \sim Q_{X}}(h(x)=1) - Pr_{x \sim P_{X}}(h(x)=1)| = d_{H}(Q_X, P_X)\)
- Lemma
\(\displaystyle d_{H}(Q_X, P_X)\) can be estimated by m samples from source and target domains.
\(\displaystyle VC(H)=d\) then with probability \(\displaystyle 1-\delta\)
\(\displaystyle d_{H}(Q_X, P_X) \leq d_{H}(Q_{X}^{(m)}, P_{X}^{(m)}) + 4 \sqrt{\frac{d \log(2m) + \log(2/\delta)}{m}}\)
- Label source examples as 1 and label target samples as 0.
- Train a classifier to classify source and target.
- If loss is small then divergence is large. \(\displaystyle \frac{1}{2} d_{H}(Q_X^{(m)}, P_X^{(m)}) = 1-loss_{class}\)
Recap
Beginning of Lecture 18 (Oct. 29, 2020)
Given labeled examples from the source domain: \(\displaystyle Q_{X,Y} = \{(x_i^S, y_i^S)\}_{i=1}^{m_s}\).
Target domain: \(\displaystyle P_{X} = \{x_i^t\}_{i=1}^{m_t}\).
Learn a function \(\displaystyle h \in H\).
\(\displaystyle \epsilon^T(h) = E_{(x,y) \sim P_{X,Y}}[ l(h(x), y) ]\).
H-divergence:
\(\displaystyle d_H(Q_X, P_X) = 2\sup_{h \in H} | P_{Q}(h(x)=1) - P_{P}(h(x)=1)| = 2(1-loss_{classifier})\).
This can be estimated by training a classifier to distinguish between train and test samples.
Def:
For the hypothesis class H, the symmetric difference hypothesis space \(\displaystyle H \triangle H\) is the set of disagreements between any two hypothesis in H:
\(\displaystyle H \triangle H = \{g(x) = h(x) \oplus h'(x) \mid \forall h, h' \in H\}\).
- Main Result
\(\displaystyle H\) is a hypothesis class with \(\displaystyle VC(H)=d\).
With probability \(\displaystyle 1-\delta\), \(\displaystyle \forall h \in H\):
\(\displaystyle \epsilon_{T}(h) \leq \epsilon_{S}(h) + \frac{1}{2} d_{H \triangle H}(Q_X^{(m)}, P_X^{(m)}) + \epsilon_{joint}\).
Target error is <= source error + divergence
Practical Domain Adaptation Methods
- Classical DA methods (pre deep learning)
- Metric Learning
- Subspace alignment
- MMD-based distribution matching
- Sample reweighting & selection
- Modern DA methods (i.e. deep domain adaption)
Ganin & Lempitsky
The idea is to train an embedding function using an adversarial domain classifier to extract common features from the source and target domains.
- Input \(\displaystyle x\) goes to an embedding function \(\displaystyle F\) to get features.
- Features go to a classification network \(\displaystyle C_1\) to get labels.
- Features also go to a domain classifier \(\displaystyle C_2\).
- Training: \(\displaystyle \min_{F, C_1, C_2} E_{(x, y)} \sim Q_{X,Y}^{(m)} [\ell(C_1 \circ F(x), y)] - \lambda L(C_2)\).
- In general, we want to find a mapping (embedding) \(\displaystyle F\) such that \(\displaystyle F(Q_X) \approx F(P_X)\).
- The domain classifier penalizes the distance between \(\displaystyle F(Q_X)\) and \(\displaystyle F(P_X)\).
Example 1: MMD distance (Maximum mean discrepancy)
Define \(\displaystyle \tilde{x}_i = F(x_i)\).
\(\displaystyle D_{MMD}(Q^{(m)}_{\tilde{x}}, P^{(m)}_{\tilde{x}}) \stackrel{\triangle}{=} \Vert \frac{1}{m}\sum \phi(\tilde{x}_i^S) - \frac{1}{m}\sum \phi(\tilde{x}_i^T) \Vert\)
Here \(\displaystyle \phi: \mathbb{R}^r \to \mathbb{R}^D\) is a fixed kernel function.
We square D to apply the kernel trick:
\(\displaystyle D^2_{MMD}(Q^{(m)}_{\tilde{x}}, P^{(m)}_{\tilde{x}}) = \frac{1}{m^2}\left( \sum_{i,j=1}^{m}K(x_i^s x_j^s) + \sum_{i,j=1}^{m}K(x_i^t, x_j^t) - 2 \sum_{i,j=1}^{m}K(x_i^t, x_j^t) \right)\)
MMD-based DA (Tzeng et al. 2014):
\(\displaystyle \min L(c_1 \circ F(x^s, y^s) + \lambda D^s_{MMD}(F(x^s, F(x^t))\)
Example 2: Wasserstein distance
\(\displaystyle \min L_{cls}(C_1 \circ F(x^S), y^s) + \lambda W(F(x^s, F(x^s))\)
The wasserstein distance is computed using the Kantorovich duality.
This is also called IPM (Integral prob. metrics) distance.
- We can also use improved & robust version of Wasserstein in DA.
- Robust Wasserstein [Balaji et al. Neurips 20]
- Normalized Wasserstein [....ICCV]
CycleGAN
[Zhu et al 2017]
Another approach for image-to-image translation.
Source: \(\displaystyle (x^s, y^s)\)
Target: \(\displaystyle x^t\)
Train two functions: \(\displaystyle G_{S \to T}\) and \(\displaystyle G_{T \to S}\).
Losses:
- \(\displaystyle L_{GAN}(x^S, x^T, G_{S\to T}(D^T) = E_{x^t}\left[\log D^T(x^t)\right] + E\left[\log(1-D^T(G_{S\ to T}(x^s)) \right]\).
- \(\displaystyle L_{GAN}(x^S, x^T, G_{T \to S}(D^S)\)
- Cycle consistency: \(\displaystyle L_{cyc} = E\left[ \Vert G_{T\to S}(G_{S \to T}(x^s)) - x^s \Vert \right] + E \left[ \Vert G_{S \to T}(G_{T\ to S}(x^t)) - x^t \Vert \right]\)
Other tricks:
- Domain-specific batch norms
- Entropy based regularization
Are assumptions necessary?
Assumptions:
- Covariate shift
- \(\displaystyle d_H(Q_x, P_x)\) is small
- \(\displaystyle \epsilon_{joint}\) small
See [Ben-David et al.].
- Covariate shift assumption is not sufficient.
- Necessity of small \(\displaystyle d_{H}(P,Q)\) for DA.
- Necessity of small joint training error.
Domain Generalization
Also known as out-of-dist (OOD) generalization.
Training: \(\displaystyle |E|\) training domains (envs)
\(\displaystyle P^{(e)} \sim \{(x_i^e, y_i^e)\}_{i=1}^{m_e}\) with \(\displaystyle 1 \leq e \leq |E|\).
Goal: Find \(\displaystyle h \in H\) that performs well in an unseen domain (domain \(\displaystyle |E|+1\)).
At test time \(\displaystyle P^{(K+1)} \sim \{(x_i^{(k+1)}, y_i^{(k+1)})\}_{i=1}^{m_{(k+1)}} = E[\ell(h(x),y)]\).
\(\displaystyle R^{(k+1)}(h) = E_{(x,y) \sim P^{(k+1)}}[\ell(h(x), y)]\).
- Example datasets
- DomainNet
- 6 domains: painting, photo, sketches, drawings, clipart, infograph
- PACS
- 4 domains: art, cartoon, photo, sketch
- Some Simpler datasets
- Rotated MNIST
- Color MNIST
One generalization method is to do nothing, just training normally with ERM.
Domain-adversarial neural networks (DANN)
- Train a feature extractor \(\displaystyle \phi\) and a classifier \(\displaystyle w\) to yield \(\displaystyle f=w \circ \phi\).
- Domain classifier \(\displaystyle c\).
- \(\displaystyle loss = \frac{1}{k} \sum_{j=1}^{k} E[\ell(w \circ \phi(x), y)] + \lambda L(domain\_classification)\).
- We optimize \(\displaystyle \min_{\phi, w} loss\)
- We can use Wasserstein distance:
- \(\displaystyle loss = \frac{1}{k} \sum_{j=1}^{k} E[\ell(w \circ \phi(x), y)] + \lambda \sum w(P_{X|Y}^{j_1}, P_{X|Y}^{j_2})\)
- This is solved using alternating gradient descent.
Meta Learning for Domain Generalization
[Li et al. 2017]
Idea: Build meta-test domains
- Meta-train
- Loss: \(\displaystyle L_{meta\_train(\theta) = \frac{1}{K-K_1} \sum_{j} E[\ell(f_{\theta'}(x), y)]\)
- Take one-gradient step to update the model:
- \(\displaystyle \phi' = \phi - \eta \nabla L_{metatrain}(\theta)\)
Overall objective:
- \(\displaystyle \min_{\theta} L_{\text{meta-train}}(\theta) + \beta L_{\text{meta-test}}(\theta')\)
To update \(\displaystyle L_{meta}(\theta)\), we need to compute \(\displaystyle \nabla L_{meta}(\theta)\) which depends on the Hessian wrt \(\displaystyle \theta\). This can be solved using a hessian-vector product without computing out the hessian which could be very large.
Invariant Risk Minimization (IRM)
[Arjovsky et al. (2019)]
Idea: Find a feature extractor \(\displaystyle \phi()\) such that optimal classifier is the same for every domain.
Define: \(\displaystyle R^e(\phi, w) = E[\ell (w_0 \phi(x), y)]\).
Objective: \(\displaystyle \min_{\phi, \hat{w}} \frac{1}{k} \sum R^e (\phi, w)\) s.t. \(\displaystyle \forall e\), \(\displaystyle \hat{w} \in \operatorname{argmin}_{\beta} R^e(\phi, \beta)\)
This is a bi-level optimization which is difficult to solve. The constraint depends on another optimization.
The paper uses a lagrangian relaxation: \(\displaystyle \min_{\phi, \hat{w}} \frac{1}{k} \sum R^e(\phi, \hat{w}) + \lambda \Vert \nabla_{\hat{w}} R^e(\phi, \hat{w}) \Vert^2_2\).
Argument: If we can solve the optimization, such a function will use only invariant features since non-invariant features will have different conditional distribution with the label.
[Rosenfeld et al. Oct 2020]
Not a valid argument in general as IRM fails to recover invariant predictors.
Which method for generalization works the best?
[Gultajani & Lopez-Poz] offer the following empirical observations:
- Model selection is critical in domain generalization.
- Training-domain validation set
- Leave-one-domain out validation set
- Oracle selection
- Data augmentation is important in domain generalization
- random crops, random horizontal flips, random color jitter
- image-to-image neural translation
- ERM (doing nothing) outperforms other DG methods!!
- Possible with careful model selection
- Larger models help with domain generalization.
- See DomainBED for code and data.
Self-supervised Learning
Lecture 21 (November 10, 2020)
Given data \(\displaystyle x\), we want to find a good representation \(\displaystyle f(x)\).
We can use \(\displaystyle f(x)\). to solve the classification problem more efficiently (e.g. using linear classifiers).
Task 1: Learn a good \(\displaystyle f(x)\) from unlabeled samples.
Task 2: Use \(\displaystyle f(x)\) + a few labels to solve classification problem using linear models.
Note that in semi-supervised learning, you have unlabeled examples and a few labelled examples but you know what the task is.
In self-supervised learning, we use structure in labelled data to create artificial supervised learning problems solved via deep models.
In this process, the learning method hopefully will create internal representations for the data \(\displaystyle f(x)\) useful for downstream tasks.
Image embedding
Surprising observation for image embedding:
[Gidaris et al. ICLR 2018] + [Zhang et al. 2019]
- Rotate images and use the angle of rotation as labels (e.g. \(\displaystyle \theta = 0, 90, 180, 270\)).
- Train a CNN to predict the rotation angle from images.
- Use \(\displaystyle f(x)\) with linear classification models for the true labels.
- Why should \(\displaystyle f(x)\) be a good representation for images?
This is an open question.
Contrastive Learning
[Logeswaren & Lee ICLR 2018] use a text corpus (Wikipedia) to train deep representation \(\displaystyle f(x)\):
\(\displaystyle x, x^{+}\) are adjacent sentences.
\(\displaystyle x, x^{-}\) are random sentences.
Optimization: \(\displaystyle \min_{f} E[\log(1 + \exp^{f(x)^T f(x^-) - f(x)^T f(x^+)]})] \approx E[f(x)^T f(x^-) - f(x)^T f(x^+)]\). This is known as contrastive learning.
Sentence embeddings capture human notions of similarities:
E.g. the tiger rules this jungle is similar to a lion hunts in a forest.
- Can we use contrastive learning to obtain power data representations for images?
We need pairs of similar images and dissimilar images.
- SimCLR [Chen et al. 2020]
- Create two correlated views of an image \(\displaystyle x\): \(\displaystyle \tilde{x}_i\) and \(\displaystyle \tilde{x}_j\).
- Random cropping + resize
- Random color distortion
- Random Gaussian blur
- Use base encoder (ResNet) to map \(\displaystyle \tilde{x}_i,\tilde{x}_j\) to embeddings \(\displaystyle h_i, h_j\).
- Train a project head \(\displaystyle g()\) (one hidden layer MLP) to map h's to z's which maximize the agreement between z's.
- Loss function: \(\displaystyle sim(z_i, z_j) = \frac{z_i^t z_j}{\Vert z_i \Vert \Vert z_j \Vert}\)
Randomly select \(\displaystyle N\) samples and add their augmentations to get 2N samples.
Compute similarity matrix \(\displaystyle S \in \mathbb{R}^{2N \times 2N}\).
\(\displaystyle S_{ij}=\exp(sim(z_i, z_j)) =
\begin{cases}
1 & \text{if }i=j\\
high & \text{if }{j=2k\text{ and }i=2k-1}\\
low & otherwise
\end{cases}
\)
Training is \(\displaystyle \min_{f,g} L = \frac{1}{N} \sum_{k=1}^{N} \frac{l(2k-1,2k) + l(2k, 2k-1)}{2}\).
Practical observations:
- Composition of data augmentation is important.
- Larger batch sizes and longer training helps self-supervised learning!
- Optimization over the MLP projection head \(\displaystyle g\) helps!
- f is able to keep some information useful for the classification (e.g. color or orientation)
Empirical results:
- For image net, top-1 accuracy increases as number of parameters increases.
- After learning embeddings \(\displaystyle f\), you don't need much labeled data for supervised-training.
Theory of self-supervised learning
- [Arora et al. 2019]
Modeling of similar pairs:
- \(\displaystyle x \sim D_{C1}(x)\)
- \(\displaystyle x^+ \sim D_{C1}(x)\) is semantically similar
- \(\displaystyle x^- \sim D_{C2}(x)\) negative samples
Downstream task:
- pairwise classification
- nature picks two classes C1, C2
- generate samples from C1 & C2 and evaluate the classification loss
- Assume \(\displaystyle m \to \infty\) so just look at population loss
Notations:
- \(\displaystyle L_{sup}(f)\) is the supervised learning loss with optimal last layer
- \(\displaystyle l=E_{(x, x^+) \sim D_{sim}, x^- \sim D_{net}}[\log(1+\exp(f(x)^T f(x^-) - f(x)^Tf(x^+)]\) is a logistic loss
Result 1:
- \(\displaystyle L_{sup}^{mean}(f) \leq \frac{1}{1-\tau}(L_{un}(f)-\tau)\) for all \(\displaystyle f \in F\)
- \(\displaystyle \tau\) is the collision probability for pair of random classes.
Idea result:
- \(\displaystyle L_{sup}(f^*) \leq \alpha L_{sup}(f)\) forall \(\displaystyle f\).
- In general it is impossible to get this.
- [Tosh et al. 2020]
This work connects self-supervised learning with multi-view representation theory.
Start with (x, z, y) where x,z are two views of the data and y is the label.
- x and z should share redundant information w.r.t. y. I.e. predicting y from x or z individually should be equivalent to predicting y from both.
- \(\displaystyle e_x = E(E[Y|X] - E[Y|X,Z])^2\) and \(\displaystyle e_z = E(E[Y|Z] - E[Y|X,Z])^2\) should be small
- Formulate contrastive learning as an artificial classification problem:
- Classify between \(\displaystyle (x, z, 1)\) and \(\displaystyle (x, \tilde{z}, 0)\).
- \(\displaystyle g^*(x,z) = \operatorname{argmin}(\text{classification loss}) = \frac{P_{X,Z}(x,z)}{P_X(x) P_Z(z)}\).
- x,z have redundant info from Y so if we first predict z from x, then use the result to predict Y, we should be good
\(\displaystyle \begin{aligned} \mu(x) &= E[E[Y|Z]|X=x] \\ &= \int E[Y|Z=z] P_{Z|X}(z|x) dz\\ &= \int E[Y|Z=z] g^*(x,z) P_Z(z) dz \end{aligned} \)
Lemma: \(\displaystyle E[(\mu(x) - E[Y | x,z])^2] \leq e_x + e_z + 2\sqrt{e_x e_z}\)
Landmark embedding: \(\displaystyle g^*\) is computed via contrastive learning.
How to embed x? \(\displaystyle \phi(x) = (g^*(x, z_1),...,g^*(x,z_m))\)
z's are randomly generated from \(\displaystyle P_Z\).
Each \(\displaystyle g^*\) output is a single number.
- \(\displaystyle \phi()\) is good embedding if a linear classifier of \(\displaystyle \phi\) is approx \(\displaystyle \mu(x)\).
- I.e. \(\displaystyle \exists w : w^t \phi(x) \approx \mu(x)\)
- \(\displaystyle w^t \phi(x) = \frac{1}{m} \sum_{i=1}^{m} E[Y|Z_i] g^*(x, z_i) \stackrel{m \to \infty}{\rightarrow} \int E[Y|Z=z] g^*(x,z)P_{Z}*z dz = \mu(x)\)
Direct embedding
Instead of learning a bivariate \(\displaystyle g(x,z)\), learn \(\displaystyle \eta(x)^T \psi(z)\).
Lemma: For every \(\displaystyle \eta: x \to \mathbb{R}^m\) and \(\displaystyle \psi:z \to \mathbb{R}^m\), there exists \(\displaystyle w \in \mathbb{R}^m\) such that \(\displaystyle E[(w^t \eta(x) - \mu(x))^2] \leq E[Y^s \epsilon_{direct}(\eta, \psi)\) where \(\displaystyle \epsilon_{direct} = [(\eta(x)^t \psi(x) - g^*(x,z))^2\).
Can we write \(\displaystyle g^*(x,z)\) as \(\displaystyle \eta(x)^T \psi(z)\)?
- If there is a hidden variable H s.t. X and Z are conditionally independent given H.
- Case 1: H is a discrete variable then \(\displaystyle g^*(x, z) = \eta^*(x)^t \psi(z^*)\)
- Case 2: There exists \(\displaystyle \eta,\psi\) such that \(\displaystyle E(\eta(x)^t \psi(z) - g^*(x,z))^2 \leq o(\frac{1}{m})\).
Meta Learning
In many applications, we don't have a large training dataset. However, humans can adapt and learn on the fly.
The key is to use prior knowledge in performing new tasks.
How can we train AI/ML models similarly?
Goal of meta learning: Train a model on different learning tasks such that it can solve new tasks using only a small number of training samples.
Few shot classification problem:
Inputs: \(\displaystyle D_{metatrain} = \{(D_i^{train}, D_i^{test})\}_{i=1}^{n}\).
\(\displaystyle
\begin{cases}
D_{i}^{train} = \{(x_j^i, y_j^i) \}_{j=1}^{k}\\
D_{i}^{test} = \{(x_j^i, y_j^i) \}_{j=1}^{k'}
\end{cases}
\)
- \(\displaystyle i\) is the index of the task
- \(\displaystyle j\) is the index of the sample
K-shot classification means k training samples per label. Some papers use k as the size of the whole training set.
Q: How to use \(\displaystyle D_{metatrain}\) to solve meta-test tasks more effectively?
- Use \(\displaystyle D_{metatrain}\) to learn meta parameters \(\displaystyle \theta\) such that:
- Base learner \(\displaystyle A\) outputs task-specific model parameters \(\displaystyle \phi_i = A(D_{i}^{train}, \theta)\) good for \(\displaystyle D_{i}^{test}\).
- Training procedure:
- Loss: \(\displaystyle \min_{\theta} \sum_{i=1}^{n} loss(D_{i}^{test}, \phi_i)\) where \(\displaystyle \phi_i = A(D_{i}^{train}, \phi)\).
- Test time: given a new task \(\displaystyle (D^{train}, D^{test})\). Apply \(\displaystyle A(D^{train}, \theta^*)\) to get \(\displaystyle \phi\).
[Fin et al. 2017]
- Idea: train a model that can be easy to fine-tune on new tasks
- one-step fine tuning: \(\displaystyle \theta - \alpha \nabla L(\theta, D_{i}^{train})\) gives us \(\displaystyle \phi_{i}\)
- Evaluate \(\displaystyle \phi_i\) on \(\displaystyle D_i^{test}\)
- \(\displaystyle \min_{\theta} \sum_{i=1}^{n} L(\phi_i, D_i^{test}) = L(\theta - \alpha \nabla L(\theta, D_i^{train}), D_i^{test})\)
1. Model-agnostic meta learning (MAML)
- Use GD to optimize over \(\displaystyle \theta\)
- \(\displaystyle \nabla_\theta = \sum_{i=1}^{n}(\nabla_{\theta} \phi_i) \nabla_{\phi} L(\phi_i, D_i^{test})\)
- \(\displaystyle (\nabla_{\theta} \phi_i)\) involves second-order derivatives which are expensive.
- First-order MAML: just ignore \(\displaystyle \nabla_{\theta} \phi_i\) term. Replace it with the identity matrix.
Reptile (Michal et al 2018) 2. \(\displaystyle A\) is a simple linear/non-parametric learning on data embeddings computed via \(\displaystyle f_{\theta}\)
[Lee et al. 2019]
- \(\displaystyle f_{\theta}\) is used to compute embeddings
- \(\displaystyle A\) is a linear classifier (e.g. SVM)
- Use dual form of SVM so # of optimization variables = # training samples * # classes
3. \(\displaystyle A\) is a non-parametric learning
- Embedding: \(\displaystyle \tilde{x} = f_{\theta}(x)\)
[Snell et al. 2017)
- Define prototypes (cluster centers)
- \(\displaystyle c_k = \frac{1}{|D_i^{tr}|} \sum_{(x,y) \in S_k} f_{\theta}(x)\)
- \(\displaystyle P_{\theta}(y=k|x) = \frac{\exp(-d(f_{\theta}(x), c_k))}{\sum_{k'} \exp(-d(f_{\theta}(x), c_k))}\)
4: \(\displaystyle A\) is a black box (e.g. LSTM).
LSTMs and transformers
Lecture 23 (November 19, 2020)
Recurrent Neural Networks (RNNs)
Hidden state: \(\displaystyle h_t = \tanh(W_{hh} h_{t-1} + W_{xh} x_t)\)
Prediction at t: \(\displaystyle y_t = W_{hy} h_{t}\)
- Backpropagation through time
If \(\displaystyle W\) has largest singular value < 1, then gradient vanishes.
If \(\displaystyle W\) has largest singular value > 1, then gradient explodes.
Typically, gradient vanishes because of initialization of \(\displaystyle W\).
Long Short Term Memory (LSTMs)
Goal is to solve the vanishing and exploding gradient problem.
LSTM has several gates:
- Input gate: \(\displaystyle i_t = \sigma(W_{xi}x_t + W_{hi}h_{t-1} + b_i)\)
- Forget gate: \(\displaystyle f_t = \sigma(W_{xf}x_t + W_{hf}h_{t-1} + b_f)\)
- Output Gate: \(\displaystyle o_t = \sigma(W_{xo}x_t + W_{ho}h_{t-1} + b_o)\)
- Cell state: \(\displaystyle c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t\)
- Hidden state: \(\displaystyle h_t = o_t \odot \tanh(c_t)\)
- Bidirectional RNNs
First LSTM takes input in correct order.
Second LSTM takes input in reverse order.
Concatenate outputs from both LSTMs.
Attention
Goal: To help memorize long source sentences in machine translation.
- Encoder-decoder attention
- Self-Attention
Transformer
- Positional encoding
- Self-Attention
Have queries, keys, and values.
Multiply queries with keys, pass through softmax. Then times values.
Yields attention of every work with respect to another.
Initially, transformers had n=8 heads giving 8 queries, keys, and values.
- Architecture
Stack encoders.
Interpretability
- Interpretability Methods
- Built-in model interpretability
- Feature level interpretability
- Instance based explanations
We will focus on feature level interpretability.
Feature Level Interpretability
These are given through saliency maps.
- Perturbation-based: Perturb the input to get another output and compute the difference.
- Gradient-based
Gradient-based Methods
Take the derivative of the output with respect to the input.
- Limitations
- Too local and sensitive to slight perturbations
- Saturated outputs lead to unintuitive gradients
- Discontinuous gradients are problematic
- SmoothGrad
- Add gaussian noise to input and average the gradient.
- Integrated Gradients
- Average the gradients along path from baseline to input.
- DeepLift
- We don't care about gradient but the slope relative to the reference state
- Limitations
- Models must be able to compute the gradient of the output with respect to the input
- Interpretation of neural networks is fragile
- Saliency maps are uninterpretable for adversarial examples on clean models and adversarially trained models.
- Needs white-box gradient access to the model.
Evaluation of interpretability methods
- Human evaluation
- Can humans evaluate saliency?
- Accuracy drop after removing salient features
- Sanity checks
- Model parameter randomization test - compare output of saliency method on trained vs untrained method to make sure saliency depends on model parameters.
- Synthetic Data
- Data randomization test
- Train on random labels and see if saliency depends on relationship between input & output.
Temporal saliency Rescaling
- If you remove this feature, how is the gradient going to change.
Reinforcement Learning
Lecture 27 (December 1, 2020)
- Goal
- Sequential decision making problems
- Current decisions can affect future decisions
Examples: games, robotics, self-driving, finance
Agent takes an action \(\displaystyle a_t\) in the environment which leads to a new state \(\displaystyle \delta_{t+1}\).
- Definitions
- \(\displaystyle S\) is the state space. This can be discrete or continuous.
- \(\displaystyle O\) are the observations.
- \(\displaystyle A\) is the set of actions which can be discrete or continuous.
- \(\displaystyle P\) are the transition probabilities which model the environment.
Example:
- \(\displaystyle |S|\) = 2
- \(\displaystyle |A|\) = 2
In general, \(\displaystyle S_t \sim P(S_t=s | s_0, a_0, s_1, a_1, ..., a_{t-1})\).
The given variables are the trajectory \(\displaystyle T_{t-1}\).
Modeling this can be very complex for large \(\displaystyle T\).
Thus, we apply a markov assumption:
- \(\displaystyle S_t \sim P(S_t=s | a_{t-1}, s_{t-1})\)
Objective: To maximize the rewards
- \(\displaystyle R_t \stackrel{\triangle}{=} R(s_t, a_t)\)
Two regimes for rewards
- Finite horizon; T is finite
- Infinite horizon; T goes to infinity
- Discount factor
Classical RL
Finite Markov Decision Process (MDP)
- S: Finite number of states
- A: Finite number of actions
- \(\displaystyle R_t = R(a_t, S_t)\)
- r discount factor
Goal: Choose actions to maximize the total rewards.
- Policy function \(\displaystyle \pi\) determines how actions should be taken.
- The policy function could yield a dist on actions or can be deterministic. We will focus on deterministic actions.
- Assume this is time invariant.
- Value function determines the expected reward if we start at state s and follow policy \(\displaystyle \pi\).
- Q function (action-value function)
- \(\displaystyle Q_\pi (s, a) = E[R_0 + \gamma R_1+... | A_0=a, S_0=s, \pi]\)
- If we have \(\displaystyle \pi\), can we evaluate \(\displaystyle V_{\pi}(s)\)?
- \(\displaystyle V_{\pi}(s) = E[R_0 + \gamma R_1 + ... | S_0 = s, \pi]\)
- Use Bellman's equation
- \(\displaystyle V_{\pi}(s) = R_0 + \gamma \sum_{s'} P_{\pi}(s' | s) V_{\pi}(s')\)
- \(\displaystyle V_{\pi} = R + \gamma P_{\pi} V_{\pi}\)
- \(\displaystyle V_{\pi} = (I - \gamma P_{\pi})^{-1}R\)
- \(\displaystyle P_{\pi}\) is a stochastic matrix. It is not symmetric so eigenvalues can be complex.
All eigen values are \(\displaystyle \Vert \lambda_i \Vert \leq 1\) with one eigenvalue norm exactly 1.
This implies \(\displaystyle I - \gamma P_{\pi}\) is always invertible.
However, computing the inverse is computationally expensive since it scales with \(\displaystyle |S|^3\).
Value-Iteration (Bellman Recursion)
\(\displaystyle V_{\pi} = R + \gamma P_{\pi} V_{\pi}\)
Define an operator \(\displaystyle L_{\pi}v = R + \gamma P_{\pi}v\)
\(\displaystyle v_pi = L_{\pi} v_{\pi}\) so \(\displaystyle v_{\pi}\) is a fixed point to \(\displaystyle L_{\pi}\).
- Claim
- \(\displaystyle L_{\pi}\) is a contraction.
Proof: Take \(\displaystyle v_1, v_2 \in \mathbb{R}^d\).
\(\displaystyle
\begin{aligned}
L_{\pi}v_1 - L_{\pi}v_2 &= (R + \gamma P_{\pi}v_1) - (R + \gamma P_{\pi}v_2) \\
&= \gamma P_{\pi}(v_1 - v_2)
\end{aligned}
\)
\(\displaystyle
\begin{aligned}
\Vert L_{\pi}v_1 - L_{\pi}v_2 \Vert &= \Vert \gamma P_{\pi}(v_1 - v_2) \Vert\\
& \leq \gamma \Vert P_{\pi} \Vert \Vert v_1 - v_2 \Vert \\
& \leq \Vert v_1 - v_2 \Vert
\end{aligned}
\)
By Banach's Fixed Point Theorem, we can converge to the fixed point iteratively by repeatedly applying \(\displaystyle L_{\pi}\).
Optimal Policy
Elementwise max: \(\displaystyle \max_{\pi} v_{\pi}(s)\) leads to the optimal policy \(\displaystyle \pi^*(s)\).
Bellman (1957) showed that for an MDP, there exists an optimal policy that is deterministic and such that \(\displaystyle v_{\pi^*}(s) \geq v_{\pi}(s)\) for all \(\displaystyle s, \pi\).
The policy may not be unique but if two policies are equal, they have the same value function.
Intermediate questions:
- Given \(\displaystyle v^*\), can we compute \(\displaystyle Q^*\)?
\(\displaystyle \begin{aligned} Q^*(s, a) &= \max_{\pi} Q(s,a)\\ &= \max_{\pi} R(s) + \gamma \sum_{s'} p(s' | s,a) v_{\pi}(s')\\ &= R(s) + \gamma \sum_{s'} P(s' | s, a) \max_{\pi}(v_{\pi}(s'))\\ \end{aligned} \)
- Given \(\displaystyle Q^*\), can we compute \(\displaystyle v^*\).
Bellman's optimality states that \(\displaystyle v^*(s) = \max_{a} Q^*(s, a)\).
\(\displaystyle \pi^*(s) = \operatorname*{argmax}_{a} Q^*(s, a)\)
- How to compare optimal policies?
First approach: Value Iteration
\(\displaystyle V^*(s) = \max_{a} Q^*(s, a) = \max_{a} [R(s) + \gamma \sum_{s'} p(s'|s,a) v^*(s')]\)
Define an operator: \(\displaystyle L(v) = \max_{\pi}[R + \gamma P_{\pi} v]\)
\(\displaystyle v^*\) is a fixed point of \(\displaystyle L(v)\).
Claim: \(\displaystyle L\) is also a contraction.
Thus \(\displaystyle v^*\) can be computed by repeated application of \(\displaystyle L\).
Value Iteration
- Start with a random \(\displaystyle v^{(0)} \in \mathbb{R}^d\)
- \(\displaystyle v^{(r+1)}(s) = \max_{a} [R(s) + \gamma \sum_{s'} p(s'|s,a) v^{r}(s')]\)
- Repeat until \(\displaystyle \Vert v^{(r+1)} - v^{(r)} \Vert \leq \epsilon\)
Policy Iteration
Directly optimize policy.
- Start with a random policy \(\displaystyle \pi^{(0)}\)
- Evaluate the policy \(\displaystyle v_{\pi}\) using closed form or value iteration
- Evaluate the Q-Function \(\displaystyle Q_{\pi}(s, a) = R(s) + \gamma \sum_{s'} P(s'|s,a) V_{\pi}(s')\)
- Find the best action to be taken at state \(\displaystyle s\):
- \(\displaystyle a^*(s) = \operatorname{argmax}_{a} Q_{\pi}(s, a)\)
- Update \(\displaystyle \pi\) using \(\displaystyle \pi(s) = a^*(s)\)
- Repeat until convergence.
Policy iteration is guaranteed to converge to an optimal policy.
Oftentimes converges faster than value iteration.
Deep Reinforcement Learning
- Relaxing some unrealistic assumptions
- Evaluate \(\displaystyle v_{\pi}(s)\)
- \(\displaystyle Q_{\pi}(s, a) = R(s, a) + \gamma E_{s' \sim P(s'|s,a)} v_{\pi}(s')\)
- Improve the policy
- \(\displaystyle \operatorname{argmax}_{a_t} Q_{\pi}(s_t, a_t)\)
- Assumption \(\displaystyle |S|=d\)
- How to represent \(\displaystyle V(s)\)?
- Can we use a neural network to represent \(\displaystyle V(s)\)? Yes
- How to train \(\displaystyle v_{\phi}\)?
- Start with an old \(\displaystyle v_{\phi}\), compute \(\displaystyle Q_{\pi}(s,a)\).
- \(\displaystyle Q_{\pi}(s,a) = R(s,a) + \gamma E[v_{\phi}^{old}(s')]\)
- \(\displaystyle Q_{\pi}(s,a) = R(s,a) + \gamma E[v_{\phi}^{old}(s')]\)
- Fit \(\displaystyle v_{\phi}\) to \(\displaystyle \max_{a}Q_{\pi}(s,a)\) using a quadratic loss:
- \(\displaystyle L(\phi) = \frac{1}{2} \Vert V_{\phi}(s) - \max_{a} Q_{\pi}(s,a) \Vert^2\)
- \(\displaystyle L(\phi) = \frac{1}{2} \Vert V_{\phi}(s) - \max_{a} Q_{\pi}(s,a) \Vert^2\)
- Iterate
- Similarly we can parameterize the Q function
Compare target \(\displaystyle y_i \leftarrow R(s_i, a_i) + \gamma E[v_{\phi}(s_i')]\)
We need to know transition probabilities \(\displaystyle P(s'|s,a)\) to compute the expectation (model-based RL).
With model-free RL:
We can approximate as \(\displaystyle E[v(s_i')] \approx v(s_i') = \max_a Q(s_i', a')\)
This is called Q-Learning.
- What if we have continuous actions
- Approach 1: Use a function class such that \(\displaystyle \max_{a}Q(s,a)\) is easy to solve
- [Gu et al. 2016] use quadratic functions.
- Approach 2: Learn another network to approximate the maximizer: \(\displaystyle \max_{a} Q(s,a')\)
Policy Gradient Method
Lecture 29 (Dec 8, 2020)
Probability of observing a trajectory:
\(\displaystyle P_{\theta}(\tau) = P(s_1) \prod_{t=1}^{\tau} \pi_{\theta}(a_t | s_t) P(s_{t+1} | s_t, a_t)\)
Reward for a trajectory:
\(\displaystyle R(\tau_1) = R(s_1, a_1) + R(s_2, a_2) + ... + R(s_t, a_t)\)
The average reward is:
\(\displaystyle J(\theta) = E[R(\tau)] = \sum E[R(s_t, a_t)]\)
Our goal is to maximize the average reward: \(\displaystyle \max_{\theta} J(\theta)\).
Gradient of the average reward:
\(\displaystyle
\begin{aligned}
\nabla_{\theta} J(\theta) &= \nabla_{\theta} E[R(\tau)] \\
&= \nabla_{\theta} \int P_{\theta}(\tau) R(\tau) d\tau \\
&= \int \nabla_{\theta} P_{\theta}(\tau) R(\tau) d\tau \\
&= \int P_{\theta}(\tau) \nabla_{\theta} \log P_\theta(\tau) R(\tau) d\tau\\
&= E[\log P_\theta(\tau) R(\tau)]
\end{aligned}
\)
\(\displaystyle
\nabla_{\theta} \log P_{\theta}(\tau) = \sum_{t=1}^{\tau} \nabla_{\theta} \log \pi_{\theta}(a_t | s_t)
\)
Implies,
\(\displaystyle
\begin{aligned}
\nabla_{\theta} J(\theta) &= E[...]\\
&\approx \frac{1}{N} \sum_{i=1}^{N}(\sum \nabla_{\theta} \log \pi(a_t^{(i)} | s_t^{(i)}) ....
\end{aligned}
\)
- Summary
- Sample trajectories
- Approximate \(\displaystyle \nabla_{\theta} J(\theta)\)
- \(\displaystyle \theta \leftarrow \theta + \alpha \nabla J(\theta)\)
- Intuition
\(\displaystyle E[\nabla_{\theta} \log P_{\theta}(\tau) R(\tau)]\)
Formalizing trial & error.
[Finn & Levin, ICML]
Issues with Policy Gradient
- High variance of gradient estimation
- Solutions
- Subtract a baseline
\(\displaystyle b = \frac{1}{N} \sum_{i=1}^{N} R(\tau^{(i)})\)
- Reward-to-go
\(\displaystyle \begin{aligned} \nabla_{\theta} J(\theta) &\approx \frac{1}{N} \sum_{i=1}^{N} \nabla_{\theta} \log P_{\theta}(\tau) R(\tau)\\ &= \frac{1}{N} \sum_{i=1}^{N} \left(\sum_{t=1}^{T} \nabla_{\theta} \pi_{\theta}(a_t^{(i)}| s_t^{(i)}) \right) \left(\sum_{t'=1}^T R(s_{t'}^{(i)}, a_{t'}^{(i)})\right)\\ &= \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \pi_{\theta}(a_t^{(i)}| s_t^{(i)}) \left(\sum_{t'=1}^T R(s_{t'}^{(i)}, a_{t'}^{(i)})\right)\\ &\approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \pi_{\theta}(a_t^{(i)}| s_t^{(i)}) \left(\sum_{t'=t}^T R(s_{t'}^{(i)}, a_{t'}^{(i)})\right)\\ \end{aligned} \)
- Some parameters can change \(\displaystyle \pi_{\theta}\) more than others so it's hard to choose a fixed learning rate.
Use natural policy gradient: \(\displaystyle \theta' \leftarrow \theta - \eta F^{-1}\nabla L(\theta)\)
Actor-critic algorithms
Have an actor \(\displaystyle \pi_{\theta}\).
Have a critic \(\displaystyle V_{\phi}/Q\)
\(\displaystyle \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}(a_t^{(i)} | s_t^{(i)}) \left(Q(s_t^{(i)}, a_t^{(i)} - V(s_t^{(i)})\right)\)
Other topics in RL
- Inverse RL
- Multi-agent RL
- Model-based RL
Summary of Course
- What we covered
- Supervised DL
- Unsupervised DL (GANs, VAEs)
- Self-supervised DL
- Meta-Learning
- Learning with Attention (Transformers)
- Deep RL
- Optimization
- Generalization
- Robustness
- Interpretability
- What we didn't cover
- Fairness
- Privacy & Ethics
- Bayesian DL
- Federated Learning
- Graph NNs
- Things which may be on the final
- Transformers
- Wasserstein distance
- Kernel methods
Resources
<templatestyles src="Reflist/styles.css" />
- ↑ Jump up to: 1.0 1.1 Chaoyue Liu, Libin Zhu, Mikhail Belkin (2020). Toward a theory of optimization for over-parameterized systems of non-linear equations: the lessons of deep learning https://arxiv.org/abs/2003.00307
- ↑ Simon S. Du, Xiyu Zhai, Barnabas Poczos, Aarti Singh (2019). Gradient Descent Provably Optimizes Over-parameterized Neural Networks (ICLR 2019) https://arxiv.org/abs/1810.02054
- ↑ Daniel Soudry, Elad Hoffer, Mor Shpigel Nacson, Suriya Gunasekar, Nathan Srebro (2018) The Implicit Bias of Gradient Descent on Separable Data The Journal of Machine Learning Research 2018 https://arxiv.org/abs/1710.10345
- ↑ Jump up to: 4.0 4.1 Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, Oriol Vinyals (2017) Understanding deep learning requires rethinking generalization (ICLR 2017) https://arxiv.org/abs/1611.03530
- ↑ Mikhail Belkin, Daniel Hsu, Siyuan Ma, Soumik Mandal (2019) Reconciling modern machine learning practice and the bias-variance trade-off (PNAS 2019) https://arxiv.org/abs/1812.11118
- ↑ Yiding Jiang, Behnam Neyshabur, Hossein Mobahi, Dilip Krishnan, Samy Bengio (2019) Fantastic Generalization Measures and Where to Find Them https://arxiv.org/abs/1912.02178
- ↑ Tianyu Gu, Brendan Dolan-Gavitt, Siddharth Garg (2017) BadNets: Identifying Vulnerabilities in the Machine Learning Model Supply Chain https://arxiv.org/abs/1708.06733
