Deep Learning
Notes for CMSC 828W: Foundations of Deep Learning (Fall 2020) taught by Soheil Feizi.
Basics
A refresher of Machine Learning and Supervised Learning.
Empirical risk minimization (ERM)
Minimize loss function over your data: \(\displaystyle \min_{W} \frac{1}{N} \sum_{i=1}^{N} l(f_{W}(x_i), y_i))\)
Loss functions
For regression, can use quadratic loss: \(\displaystyle l(f_W(x), y) = \frac{1}{2}\Vert f_W(x)-y \Vert^2\)
For 2-way classification, can use hinge-loss: \(\displaystyle l(f_W(x), y) = \max(0, 1-yf_W(x))\)
For multi-way classification, can use cross-entropy loss:
\(\displaystyle g(z)=\frac{1}{1+e^{-z}}\)
\(\displaystyle \min_{W} \left[-\sum_{i=1}^{N}\left[y_i\log(y(f_W(x_i)) + (1-y_i)\log(1-g(f_W(x_i))\right] \right]\)
Nonlinear functions
Given an activation function \(\phi()\), \(\phi w^tx + b\) is a nonlinear function.
Models
Multi-layer perceptron (MLP): Fully-connected feed-forward network.
Optimization
Apply gradient descent or stochastic gradient descent to find \(W^*\).
Stochastic GD:
- Sample some batch \(B\)
- \(w^{(t+1)} = w^{(t)} - \eta \frac{1}{|B|} \sum_{i \in B} \nabla_{W} l(f_{W}(x_i), y_i)\)
Optimizers/Solvers:
- Momentum
- RMSProp
- Adam
DL Optimization
(Lectures 2-3, September 3)
The role of "over-parameterization".
In general, you can have poor local minimums and saddle points (with pos+neg Hessian).
However, in practice GD & SGD work pretty well.
Lecture 2 (Sept 3) is about Liu et al. [1].
Suppose we have a classification problem with \(c\) labels and \(N\) samples total. This gives us \(n=N*c\) constraints.
Interpolation is possible if the number of parameters \(m\) is greater than the number of samples \(n=N*c\).
This is called the over-parameterized regime.
In the exact interpolation regime, we have: \[ \begin{aligned} f_W(x_1) &= y_1 = \begin{bmatrix} 0 \\ \vdots \\ 1 \end{bmatrix} \in \mathbb{R}^c\\ &\vdots\\ f_W(x_1) &= y_1 = \begin{bmatrix} 0 \\ \vdots \\ 1 \end{bmatrix} \in \mathbb{R}^c\\ \end{aligned} \] This can be rewritten as \(\displaystyle F(w)=y\) where x is implicit.
In the under-parameterized regime, we get poor locals. (See Fig 1a of [1]).
The poor-locals are locally convex in the under-parameterized regime but not in the over-parameterized.
Over-parameterized models have essential non-convexity in their loss landscape.
Minimizers of convex functions form convex sets.
Manifold of \(w^*\) have some curvature.
Manifold of \(w^*\) should be an affine subspace. This is in general for non-linear functions.
So we cannot rely on convex analysis to understand over-parameterized systems.
Instead of convexity, we use PL-condition (Polyak-Lojasiewicz, 1963):
For \(\displaystyle w \in B\), \(\displaystyle \frac{1}{2}\Vert \nabla L(w) \Vert^2 \geq \mu L(w)\) which implies exponential (linear) convergence of GD.
Tangent Kernels
Suppose our model is \(F(w)=y\) where \(w \in \mathbb{R}^m\) and \(y \in \mathbb{R}^n\).
Then our tangent kernel is:
\[K(w) = \nabla F(w) \nabla F(w)^T \in \mathbb{R}^{n \times n}\]
where \(\nabla F(w) \in \mathbb{R}^{n \times m}\)
Theorem 4.1 (Uniform conditioning implies PL* condition)
If \(\lambda_{\min} (K(w)) \geq \mu\) then \(\mu\text{-PL*}\) on \(B\).
\(\displaystyle \begin{aligned} \frac{1}{2}\Vert \nabla f(w) \Vert^2 &= \frac{1}{2}\Vert (F(w)-y)^T \nabla F(w)\Vert^2\\ &=\frac{1}{2}(F(w)=y)^T \nabla F(w) \nabla F(w)^T (F(w)-y)\\ &\geq \frac{1}{2} \lambda_{\min}(K(w)) \Vert F(w)-y\Vert ^2\\ &= \lambda_{\min}(K(w)) L(w)\\ &\geq \mu L(w) \end{aligned} \)
Informal convergence result:
GD converges exp fast to a solution with the rate controlled by a condition number:
\[ \kappa_{F} = \frac{\sup_{B} \lambda_{\max}(H)}{\inf_{B} \lambda_{\min}(K)}\]
Ideally we want this to be small.
\(\displaystyle F(w) = Aw = y \in \mathbb{R}^n\)
\(\displaystyle L(w) = \frac{1}{2} \Vert Aw-y\Vert^2\)
Our tangent kernel is:
\(\displaystyle K(w)=AA^T\)
and our hessian is \(\displaystyle H=A^TA\).
\(\displaystyle \kappa_{F} = \frac{\lambda_{\max}(K)}{\lambda_{\min}(K)} \geq 1\).
Our intuition is:
\(\displaystyle K=AA^T \implies E[\log K_F] \approx \log(\frac{M}{|m-n|+1})\).
So as \(\displaystyle m \to \infty\), \(\displaystyle \kappa_{F} \to 1\).
Theorem 4.2 (Local PL* implies existence of a solution + fast convergence)
Assume \(\displaystyle L(w)\) is \(\beta\)-smooth and satisfies \(\mu\)-PL condition around a ball \(\displaystyle B(w_0, R)\) with \(\displaystyle R = \frac{2\sqrt{w\beta L(w_0)}{\mu}\). Then:
- Existence of a solution: There exists a global minimum of \(\displaystyle L\), \(\displaystyle \mathbf{w}^* \in B(\mathbf{w}_0, R)\) s.t. \(\displaystyle F(\mathbf{w}^*)=\mathbf{y}\).
- Convergence of GD: GD with step size \(\displaystyle \eta = 1/\sup_{\mathbf{w}}\lambda_{\max}(H)\) converges with exponential convergence rate:
- \[L(w_t) \leq \left(1-\kappa^{-1}(B(\mathbf{w}, R))\right)^t L(\mathbf{w}_0)\]
We want to prove:
- A solution exists.
- \(\displaystyle L(w_t) \leq (1-\eta \mu)^t L(w_0)\)
Note that \(\displaystyle \eta \mu\) is the inverse of the condition number.
Beginning of Lecture 3 (September 8, 2020)
Last time (lecture 2) we expect zero training error from overparameterization.
This is the interpolation regime.
Here the number of parameters \(m\) is greater than the number of samples \(n=Nc\).
Here the manifold of \(w^*\) is the intersection of functions where \(F(w, x_1)=Y_1\) and \(F(w,x_2)=Y_2\).
Assume we use squared loss \(L(w)=\frac{1}{2}\Vert F(w)-Y \Vert^2\).
In general, our loss function is non convex, even locally.
PL-condition: If the magnitude of gradient is greater than a constant multiple \(\mu\) of loss then we say it is \(\mu\)-PL.
If our loss satisfies PL and some other conditions, then it will converge with gradient descent.
Intuition of PL
Assume:
- Loss \(\displaystyle L(w)_{w \in B}\) is \(\mu\)-PL
- Loss is \(\beta\)-smooth
- The hessian is bounded by \(\beta\)
- \(\eta=\frac{1}{\beta}\)
- Assume gradient descent: \(w_{t+1}=w_t-\mu \nabla L(w_t)\)
By Taylor's expansion:
\[
\begin{aligned}
L(w_{t+1}) &= L(w_t) + (w_{t+1}-w_t)^T \nabla f(w_t) + \frac{1}{2}(w_{t+1}-w_t)^T H(w')(w_{t+1}-w_{t})\\
&=L(w_t) + (-\eta)\nabla L(w_t)^T \nabla f(w_t) + \frac{1}{2}(-\eta)\nabla L(w_t)^T H(w')(-\eta) \nabla L(w_t)\\
&\leq L(w_t) - \eta \Vert \nabla L(w_t) \Vert^2 + \frac{\eta^2}{2} \nabla L(w_t)^T H(w') \nabla L(w_t)\\
&\leq L(w_t) - \eta \Vert \nabla L(w_t) \Vert^2 (1-\frac{\eta \beta}{2}) &\text{by assumption 3}\\
&\leq L(w_t) - \frac{\eta}{2} \Vert \nabla L(w_t) \Vert^2 &\text{by assumption 4}\\
&\leq L(w_t) - \eta \mu L(w_t) &\text{by }\mu\text{-PL assumption}\\
&= (1-\eta \mu)L(w_t)
\end{aligned}
\]
This implies our loss at any iteration is \(\displaystyle L(w_t) \leq (1-\eta \mu)^t L(w_0)\).
Thus we see a geometric or exponential decrease in our loss function with convergence rate \(\displaystyle (1-\eta \mu)\).
Similar results hold for SGD.
If we don't have convergence, we're not sure if this means we're violating the \(\mu\)-PL condition.
It is possible one of the other assumptions is violated (e.g. if learning rate is too large).
These arguments should hold for ReLU networks since the non-differentiable points are measure 0 but it would require a more careful analysis.
Caveat:
Here we assume our loss is in a ball \(\displaystyle B(w_0, R) = \{w | \Vert w - w_0 \Vert \leq R\}\) where \(\displaystyle R \leq \frac{2\sqrt{2 \beta L(w_0)}}{\mu}\).
We need to show that our gradient updates never causes us to leave this ball.
The lengths of the update vectors are \(\displaystyle \Vert w_{t+1} - w_{t}\Vert = \eta \Vert \nabla L(w_t)\Vert\).
To show that we never leave the ball, we need to have an upper bound on the length of our gradients \(\displaystyle \Vert \nabla L(w_t) \Vert\).
There is a tradeoff because for PL, we want a large \(\displaystyle \mu\) to lower bound the gradients but that would require satisfying PL over a large ball. If \(\displaystyle \mu\) is small, then we have fast (large) updates but over a small ball.
From the proof above, we have:
\(\displaystyle L(w_{t+1}) \leq L(w_t) - \frac{\eta}{2} \Vert \nabla L(w_t) \Vert^2\).
We can use this to prove we are in the ball.
Why do neural networks satisfy the conditioning assumptions?
Hessian Control
We can show \(mu\)-PL by showing the smallest eigenvalue of the tangent kernel is bounded: \(\displaystyle \lambda_{\min}(K(w_0)) \geq \mu\) and \(\displaystyle \sup_{B} \Vert H(F)\Vert\).
The tangent kernel is \(\displaystyle \nabla F(w) \nabla F(w)^T\).
If hessian is bounded then gradients don't change too fast so if we are \(\displaystyle \mu\)-PL at the initialization then we are \(\displaystyle \mu\)-PL in a ball around the initialization.
Suppose we have a NN: \(\displaystyle x \in \mathbb{R} \to y\).
\(\displaystyle f(w, x) = \frac{1}{\sqrt{m}}\sum_{i=1}^{m} v_i \sigma(w_i, x)\).
- Can we prove convergence of GD for this NN?
\(\displaystyle \nabla_{w_i} f(w, x) = \frac{1}{\sqrt{m}} v_i x \sigma'(w_i x)\)
\(\displaystyle K(w, x_j, x_j) = \frac{1}{m}\sum_{i=1}^{m} v_i^2 x^2 \left(\sigma'(w_i x)\right)^2 \equiv O(1)\) are the j-th diagonal terms of the tangent kernel:
\(\displaystyle K(w) \in \mathbb{R}^{n \times n}\).
Then the trace of the tangent kernel is also \(\displaystyle O(1)\) so the eigenvalues are bounded: \(\displaystyle \Vert K(w) \Vert = O(1)\).
\(\displaystyle H_{ij} = \frac{1}{\sqrt{m}} v_i \sigma '' (w_j x) x^2 1_{i=j}\)
The hessian is a diagonal matrix. The spectral norm of the hessian (the maximum eigenvalue) is the maximum of the diagonal elements:\\
\(\displaystyle \Vert H \Vert_2 = \max_{i \in [m]} H_{ii} = \frac{x^2}{\sqrt{m}} \max_{i \in [m]} | v_i \sigma '' (w_j x)| = O(\frac{1}{\sqrt{m}})\)
As m goes to infinity, our hessian \(\displaystyle H\) goes to 0 and tangent kernel \(\displaystyle K\) goes to a constant.
Thus Hessian control implies convergence of GD/SGD.
- However this argument assumes the model is almost linear.
- This hessian control can be extended to L-layer NN with \(\displaystyle m=\omega(\frac{n}{\mu})\)
Example:
\(\displaystyle g(w, x) = \phi(\frac{1}{\sqrt{m}}\sum_{i=1}^{m}v_i \sigma(w_i x))\)
then
- \(\displaystyle \Vert K(w) \Vert = O(1)\)
- \(\displaystyle \Vert H \Vert = O(1)\) if \(\displaystyle (\phi'' \neq 0)\)
so we cannot use hessian control.
- Lemma
If f is mu-PL then \(\displaystyle \phi \circ f\) is \(\displaystyle \mu \rho^2\)-PL (\(\displaystyle | \phi'(f(w,x))| \gt \phi\)).
implies \(\displaystyle L(w_t) \leq (1- \eta \mu \rho^2)L(w_0)\).
GD converges even though our model does not go to a linear model.
Takeaway
Over-parameterization does not lead to linearization. Over-parameterization leads to good conditioning which leads to PL and convergence of GD/SGD.
Other papers:
- Simon Du et al.[2]
Start of Lecture 4 (Sept 10)
This lecture is about Soudry et al.[3].
Setup:
- Binary classification
- Data is linearly separable
- No bias term (b=0)
Why do we pick \(w^*\) to be the max-margin solution?
To have better generalization.
We will consider functions \(f_w(x) = w^t x\) where we have \(\{(x_i, y_i)\}_{1}^{N}\), \(f_w: \mathbb{R}^d \to \mathbb{R}\), \(x_i \in \mathbb{R}^d\) and \(y_i \in \{-1, 1\}\).
We can use one of the loss functions:
- hinge loss \(l(x)=\max(1-x, 0\))
- logistic loss \(l(u) = \log(1+e^{-u})\)
- exp loss \(l(u)=e^{-u}\)
Our overall loss will be the sum of loss for each sample:
\(L(w) = \sum_{u=1}^{N}l(y_i w^t x_i)\)
Here \(x_i\) and \(y_i\) are constants so call \(\tilde{x}_i = y_i x_i\).
Now our loss is \(L(w) = \sum_{u=1}^{N}l(w^t \tilde{x}_i)\)
Assumptions:
- Data is linearly separable: \(\exists w^* \) s.t. \((w^*)^t x_i > 0\).
- \(l(u)\) is positive, differentiable, monotonically decreasing to 0, and \(\beta\)-smooth.
- Logistic and exp loss satisfy assumption 2.
Hard SVM:
Call the SVM solution \(w_{svm}^t x = 0\).
Recall the SVM optimization is:
\(\displaystyle
\begin{aligned}
\min &\Vert w \Vert^2\\
&w^t x_i \geq 1 \; \forall i
\end{aligned}
\)
We use GD to find \(w^*\):
\(\min \sum_{i=1}^{N} l(w^t x_i)\)
\(\displaystyle
\begin{aligned}
w(t+1) &= w(t) - \eta \nabla L(w(t))\\
&= w(t) - \eta \sum_{i=1}^{N} l'(w^t x_i) x_i
\end{aligned}
\)
Since the data is linearly separable, there exists \(w^*\) such that:
\((w^*)^t \nabla L(w) = \sum_{i=1}^{N} l'(w^t x_i) x_i^t w^* < 0\)
Here \(l'(w^t x_i) > 0\) and \(x_i^t w^* < 0\).
This implies there are no finite critical points (where \(\nabla L(w) = 0\).
But GD on a smooth loss converges to a critical point.
This implies \(\Vert w(t) \Vert\) goes to infinity and the loss converges to 0.
Since the loss converges to 0, GD converges to a global min.
Assumption 3: Loss function has exponential tails.
Exp and logistic loss satisfy this assumption.
- Theorem
Under assumptions 1-3, GD behaves as:
\(\displaystyle w(t) = w_{svm} \log(t) + \rho(t)\) where \(\displaystyle \Vert \rho(t) \Vert = o(\log \log t)\).
This implies \(\displaystyle \lim_{t \to \infty} \frac{w(t)}{\Vert w(t) \Vert} = \frac{w_{svm}}{\Vert w_{svm} \Vert}\).
Consider exponential loss:
\(\displaystyle l(u) = e^{-u}\)
GD in the asymptotic regime: \(\displaystyle w(t)^t x_i \to \infty\).
Lets assume the normalized w converges to a limit point \(\displaystyle w_{\infty}\):
\(\displaystyle \frac{w(t)}{\Vert w(i) \Vert} \to w_{\infty}\).
This implies \(\displaystyle w(t) = g(t) w_{\infty} + \rho(t)\).
\(\displaystyle
\begin{aligned}
-\nabla L(w) &= \sum_{i=1}^{N} \exp(-w(t)^t x_i) x_i\\
&\to \sum_{i=1}^{N} \exp(-g(t)w_{\infty}^t x_i) x_i\\
\end{aligned}
\)
Here \(\displaystyle -g(t) w_{\infty}^t x_i\) go to negative infinity since \(\displaystyle g(t) \to \infty\).
Only samples with smallest \(\displaystyle w_{\infty}^t x_i\) will contribute to the gradient:
\(\displaystyle \operatorname{argmin}_{i} w_{\infty}^t x_i\) which are exactly the support vectors.
Thus:
\(\displaystyle
\begin{aligned}
&& -\nabla L(w) &= \sum_{i \in SV} \alpha_i' x_i\\
\implies && w_{\infty} &= \sum_{i \in SV} \alpha_i'' x_i
\end{aligned}
\)
\(\displaystyle \begin{aligned} \hat{w} &= \sum_{i}^{N} \alpha_i x_i\\ \alpha_i&= 0 & x_i \notin SV\\ \alpha_i &\neq 0 & x_i \in SV\\ \end{aligned} \) These are the KKT conditions for SVM. \(\displaystyle \implies \frac{w_\infty}{\Vert w_\infty \Vert} = \frac{w_{SVM}}{\Vert w_{SVM} \Vert} \)
Rate of convergence is very slow:
\(\displaystyle \left\Vert \frac{w(t)}{\Vert w(t) \Vert} - \frac{w_{SVM}}{\Vert w_{SVM} \Vert } \right\Vert = O(\frac{1}{\log(t)})\)
Takeaway
- Even when the loss is very small, if we continue GD optimization we approach the max-margin solution which improves generalization.
- Validation or test loss may go to infinity \(\displaystyle \Omega(\log (t))\). It is better to look at the classification error in test/validation rather than the pure loss value.
- Even if validation loss is increasing, you should not stop GD because it will approach max-margin.
- More recent work
- Implicit bias exists in over-parameterized neural networks.
- Experimentally, Adam and Adagrad do not have implicit bias but have worse generalization error.
DL Generalization
Beginning of Lecture 5 (September 15, 2020).
Training set \(S = \{z^{(i)} = (x^{(i)}, y^{(i)}) \}_{i=1}^{n}\).
Our samples are from some unknown distribution: \(Z^{(i)} = (x^{(i)}, y^{(i)}) \sim P_{X, Y}\).
\(\min_{h \in H} L_{S}(h) \to h_{S}^{*}\)
In practice, we cannot compute our population loss: \(\displaystyle L_{D}(h) = E_{z \in P_{X, Y}} [l(h, z)]\).
\(\displaystyle \min{h \in H} L_{D}(h) \to h_{D}^*\).
The goal is to learn something from the training set which has a low population loss.
The estimation error is \(\displaystyle L_{D}(h_{S}^*) - L_{D}(h_{D}^*)\) where \(\displaystyle L_{D}(h_s^*)\) is the true population loss of the hypothesis gained from the test set and \(\displaystyle L_{D}(h_D^*)\) is the minimum population loss.
Classical Learning Theory
If \(\displaystyle \forall P_{X, Y}, n \geq n_0\), \(\displaystyle Pr(L_{D}(h_{S}^*) - L_{D}(h_{D}^*) \leq \epsilon) \geq 1-\delta\) then is H called PAC-learnable.
Bias-variance tradeoff
\(\displaystyle L_{D}(h_{S}^*) = L_{D}(h_{D}^*) + [L_{D}(h_{S}^*) - L_{D}(h_{D}^*)]\)
- \(\displaystyle L_{D}(h_{D}^*)\) is called the bias term, the loss of the best hypothesis in your hypothesis class. If the complexity of \(\displaystyle H\) increases, then the bias term will decrease.
- \(\displaystyle L_{D}(h_{S}^*) - L_{D}(h_{D}^*)\) is the estimation error or variance term.
- As the complexity of \(\displaystyle H\) increases, the bias decreases but the variance increases.
However, this view is not complete.
- Notations
\(\displaystyle f = l \circ h\)
\(\displaystyle L_{S}(h) = \frac{1}{n} \sum_{i=1}^{n} f(z^{(i)})\)
\(\displaystyle L_{D}(h) = E_{Z \sim P_{X, Y}}[ f(z) ] \)
\(\displaystyle F = l \circ H = \{ l \circ h, \forall h \in H \}\)
\(\displaystyle F \circ S = \left\{
\begin{bmatrix}
f(z^{(1)})\\
\vdots\\
f(z^{(n)})
\end{bmatrix}, \forall f \in F \right\}\)
Generalization error: \(\displaystyle L_{D}(h_{S}^*) - L_{S}(h_{S}^*)\)
We want to have a uniform bound on this error: \(\displaystyle G = \sup_{h \in H} L_{D}(h) - L_{S}(h)\).
We don't have the population distribution \(\displaystyle D\).
Instead, what we do is split the training data: \(\displaystyle S = S_1, \cup S_2\) with \(\displaystyle |S_1|=|S_2|=\frac{n}{2}\).
Now we have:
\(\displaystyle
\begin{aligned}
G \approx G' &=\sup_{h \in H} L_{S_1}(h) - L_{S_2}(h)\\
&= \sup_{h \in H} F(s_1) - F(s_2)\\
&= \sup_{h \in H} \frac{1}{n/2} \sum_{z^{(i)} \in S_1} f(z^{(i)}) - \frac{1}{n/2} \sum_{z^{(i)} \in S_1} f(z^{(i)})\\
&= \sup_{h \in H} \frac{2}{n} \sum_{i=1}^{n} \sigma_i f(z^{(i)}) & \text{where }\sigma_{i} = I[z^{(i)} \in S_1] - I[z^{(i)} \in S_2]
\end{aligned}
\)
We can use randomized partitioning such that \(\displaystyle \sigma = \begin{cases} 1 & \text{w.p. }1/2\\ -1 & \text{w.p. }1/2 \end{cases} \)
\(\displaystyle G \approx E_{\sigma}[G'] = \frac{2}{n} E_{\sigma} \left[ \sup_{h \in H} \sum_{i=1}^{n} \sigma_i f(z^{(i)}) \right]\)
\(\displaystyle R(A) = \frac{1}{n} E_{\sigma} \left[ \sup _a \in A \sum_{i=1}^{n} \sigma_i a_i \right]\) is called the Rademacher complexity.
Setting \(\displaystyle A = \{a_i\} = F \circ S\) \(\displaystyle \implies G \approx 2 R(F \circ S)\)
Theorem
With probability \(\displaystyle 1 - \delta\),
\(\displaystyle L_D(h) - L_{S}(h) \leq 2 R(F \circ S) + c \sqrt{\frac{\log(4/\delta)}{n}}\)
Example: \(\displaystyle H = \{ h(x) = w^t x, \Vert w \Vert_2 \leq 1\}\)
\(\displaystyle R(H \circ S) \leq \frac{\max_i \Vert x^{(i)} \Vert_2}{\sqrt{n}}\)
Question: What is the Rademacher complexity of a deep model?
\(\displaystyle H = \{ h(x) \mid h \text{ is a NN with some structure}\}\)
If \(\displaystyle R(H \circ S)\) is small then by the theorem, we can have good generalization performance.
Zhang et al.[4] perform a randomization test.
They assign random labels and observe that neural networks can fit random labels.
Recall \(\displaystyle R(H \circ S) = \frac{1}{n} E_{\sigma} \left[ \sup_{h \in H} \sum_{i=1}^{n} \sigma_i h(x_i) \right] \approx 1\)
This shows that Rademacher complexity and VC-dimension are not useful for explaining generalization for neural networks.
Theorem
There exists a two-layer NN with Relu activations and \(\displaystyle 2n+d\) parameters that can represent any function on a sample size \(\displaystyle n\) in d dimensions.
Lecture 9 (Sept 17)
From previous lecture (Zhang et al.[4]), we see that NN optimization is not much more difficult training on random labels in terms of convergence rate. Thus, Rademacher complexity and VC dimension cannot explain generalization by itself.
Examples of explicit regularization:
- Data augmentation (e.g. random crop)
- Weight decay (L2 regularization on parameters)
- Dropout
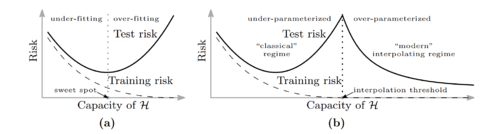
These types of explicit regularization improves generalization, but models still generalize well without them.
One reason would be implicit regularization by SGD.
Belkin et al.[5] observe that as models get more over-parameterized in the interpolation regime, test error will begin decreasing with the number of parameters. This is called double descent.
- Intuition
- In the over-parameterized regime, there are infinitely many solutions in the manifold of \(\displaystyle f_{w^*}\).
For SGD, it is easier to find simple solutions (e.g. functions with small norms). This leads to better generalization.
Can we analyze the double descent curve for some simple distributions or models?
Setup:
Our features are \(\displaystyle x = (x_1,..., x_d)\) where \(\displaystyle x_i\) are from standard normal.
Our labels are \(\displaystyle y = x^t \beta\). This is the noise-free case.
Our training set: \(\displaystyle \{(x^{(i)}, y^{(i)})\}_{i=1}^{n}\) written as \(\displaystyle X =
\begin{pmatrix}
(x^{(1)})^t\\
\vdots\\
(x^{(n)})^t
\end{pmatrix}
\)
Learning: We select \(\displaystyle p\) features: \(\displaystyle T \subseteq [d]\), \(\displaystyle |T| = P\) and fit a linear model \(\displaystyle \beta^{*}_{T} \in \mathbb{R}^{p}\), \(\displaystyle \beta^*_{T^c} =0\). Here \(\displaystyle T^c\) is the set of features we are not using.
Define \(\displaystyle X_{T} = \begin{pmatrix} (x^{(1)}_T)^t\\ \vdots\\ (x^{(n)}_T)^t \end{pmatrix} \in \mathbb{R}^{n \times P} \)
Quadratic loss: \(\displaystyle \min_{\beta_T} \Vert X_T \beta_T - y \Vert_{2}^{2} \in \mathbb{R}\).
The optimal solution is \(\displaystyle \beta_{T}^* = (X_{T}^t X_{T})^{-1} X_{T}^t y = X_{T}^{+} y\) where \(\displaystyle X_{T}^{+}\) is the Moore-penrose Pseudo-inverse.
Since we know \(\displaystyle P_{X, Y}\), we can compute the generalization error exactly.
\(\displaystyle
\begin{aligned}
E_{X,Y} \left[(y - x^t \beta^*)^2 \right] &= E \left[(x^t(\beta - \beta^*))^2\right]\\
&= E \left[(\beta - \beta^*)^t x x^t (\beta - \beta^2)\right]\\
&= (\beta - \beta^*)^t E \left[ x x^t \right] (\beta - \beta^2)\\
&= \Vert \beta - \beta^* \Vert\\
&= \Vert \beta_{T^c} \Vert^2 + \Vert \beta_{T} - \beta_{T}^* \Vert^2
\end{aligned}
\)
- Theorem
- \(\displaystyle B_{T^c} \neq 0\)
\(\displaystyle E \left[(y - x^t \beta^*)^2 \right] = \begin{cases} \Vert B_{T^C} \Vert^2 (1 + \frac{p}{n-p-1}) & p \leq n-2\\ +\infty & n-1 \leq p \leq n+1\\ \Vert B_{T} \Vert ^2 (1 - \frac{n}{p}) + \Vert B_{T^c} \Vert^2 (1 + \frac{n}{p-n-1}) & p \geq n+2 \end{cases} \)
In other cases, prescient feature selection. We can include features in \(\displaystyle T\) by decreasing the order of \(\displaystyle \beta_j^2 = \frac{1}{j^2}\). From this we get a behavior like double descent.
Related Works
Jiang et al.[6] provide some emperical evaluations of different generalization bounds such as:
- Sharpness-based bounds (PAC-Bayesian)
- Norm-based bounds
Misc
Resources
<templatestyles src="Reflist/styles.css" />
- ↑ 1.0 1.1 Chaoyue Liu, Libin Zhu, Mikhail Belkin (2020). Toward a theory of optimization for over-parameterized systems of non-linear equations: the lessons of deep learning https://arxiv.org/abs/2003.00307
- ↑ Simon S. Du, Xiyu Zhai, Barnabas Poczos, Aarti Singh (2019). Gradient Descent Provably Optimizes Over-parameterized Neural Networks (ICLR 2019) https://arxiv.org/abs/1810.02054
- ↑ Daniel Soudry, Elad Hoffer, Mor Shpigel Nacson, Suriya Gunasekar, Nathan Srebro (2018) The Implicit Bias of Gradient Descent on Separable Data The Journal of Machine Learning Research 2018 https://arxiv.org/abs/1710.10345
- ↑ 4.0 4.1 Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, Oriol Vinyals (2017) Understanding deep learning requires rethinking generalization (ICLR 2017) https://arxiv.org/abs/1611.03530
- ↑ Mikhail Belkin, Daniel Hsu, Siyuan Ma, Soumik Mandal (2019) Reconciling modern machine learning practice and the bias-variance trade-off (PNAS 2019) https://arxiv.org/abs/1812.11118
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedjiang2019generalization
