Parallel Algorithms: Difference between revisions
No edit summary |
|||
| (40 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Parallel Algorithms notes from CMSC751 with Uzi Vishkin.<br> | Parallel Algorithms notes from CMSC751 with [http://users.umiacs.umd.edu/~vishkin/index.shtml Uzi Vishkin].<br> | ||
This class is based on his book [[:File:CMSC751_Classnotes.pdf | Thinking in Parallel Some Basic Data-Parallel Algorithms and Techniques]] | This class is based on his book [[:File:CMSC751_Classnotes.pdf | Thinking in Parallel Some Basic Data-Parallel Algorithms and Techniques]]<br> | ||
[http://users.umiacs.umd.edu/~vishkin/TEACHING/ Class Website]<br> | |||
==XMT Language== | ==XMT Language== | ||
XMTC is a single-program multiple-data (SPMD) extension of C.<br> | XMTC is a single-program multiple-data (SPMD) extension of C.<br> | ||
* Spawn creates threads | |||
* Threads expire at Join | *Spawn creates threads | ||
* <code>$</code> represents the number of the thread | *Threads expire at Join | ||
* <code>PS Ri Rj</code> is an atomic prefix sum | *<code>$</code> represents the number of the thread | ||
** Stores Ri + Rj in Ri | *<code>PS Ri Rj</code> is an atomic prefix sum | ||
** Stores the original value of Ri in Rj | **Stores Ri + Rj in Ri | ||
< | **Stores the original value of Ri in Rj | ||
<syntaxhighlight lang="c"> | |||
int x = 0; | int x = 0; | ||
| Line 21: | Line 23: | ||
} | } | ||
} | } | ||
</ | </syntaxhighlight> | ||
==Models== | ==Models== | ||
| Line 32: | Line 34: | ||
====Types of PRAM==== | ====Types of PRAM==== | ||
* exclusive-read exclusive-write (EREW) | |||
* concurrent-read exclusive-write (CREW) | *exclusive-read exclusive-write (EREW) | ||
* concurrent-read concurrent-write (CRCW) | *concurrent-read exclusive-write (CREW) | ||
** Arbitrary CRCW - an arbitrary processor writing succeeds | *concurrent-read concurrent-write (CRCW) | ||
** Priority CRCW - the lowest numbered processor writing succeeds | **Arbitrary CRCW - an arbitrary processor writing succeeds | ||
** Common CRCW - writing succeeds only if all processors write the same value | **Priority CRCW - the lowest numbered processor writing succeeds | ||
**Common CRCW - writing succeeds only if all processors write the same value | |||
====Drawbacks==== | ====Drawbacks==== | ||
* Does not reveal how the algorithm will run on PRAMs with different number of proc | |||
* Fully specifying allocation requires an unnecessary level of detail | *Does not reveal how the algorithm will run on PRAMs with different number of proc | ||
*Fully specifying allocation requires an unnecessary level of detail | |||
===Work Depth=== | ===Work Depth=== | ||
| Line 51: | Line 55: | ||
;Notes | ;Notes | ||
* Other resources call this Brent's theorem | |||
* <math>x</math> is the work and <math>d</math> is the depth | *Other resources call this Brent's theorem | ||
*<math>x</math> is the work and <math>d</math> is the depth | |||
===Speedup=== | ===Speedup=== | ||
* A parallel algorithm is ''work-optimal'' if W(n) grows asymptotically the same as T(n). | |||
* A work-optimal parallel algorithm is ''work-time-optimal'' if T(n) cannot be improved by another work-optimal algorithm. | *A parallel algorithm is ''work-optimal'' if W(n) grows asymptotically the same as T(n). | ||
* If T(n) is best known and W(n) matches it, this is called ''linear-speedup'' | *A work-optimal parallel algorithm is ''work-time-optimal'' if T(n) cannot be improved by another work-optimal algorithm. | ||
*If T(n) is best known and W(n) matches it, this is called ''linear-speedup'' | |||
====NC Theory==== | ====NC Theory==== | ||
Nick's Class Theory | Nick's Class Theory | ||
* Good serial algorithms: Poly time | |||
* Good parallel algorithm: poly-log <math>O(\log ^c n)</math> time, poly processors | *Good serial algorithms: Poly time | ||
*Good parallel algorithm: poly-log <math>O(\log ^c n)</math> time, poly processors | |||
==Technique: Balanced Binary Trees== | ==Technique: Balanced Binary Trees== | ||
Example Applications: | Example Applications: | ||
* Prefix sum | |||
* Largest element | *Prefix sum | ||
* Nearest-one element | *Largest element | ||
* Compaction | *Nearest-one element | ||
*Compaction | |||
;Inputs | ;Inputs | ||
* Array A[1..n] of elements | |||
* Associative binary operation, denoted * (e.g. addition, multiplication, min, max) | *Array A[1..n] of elements | ||
*Associative binary operation, denoted * (e.g. addition, multiplication, min, max) | |||
;Outputs | ;Outputs | ||
* Array B containing B(i) = A(1) * ... * A(i) | |||
*Array B containing B(i) = A(1) * ... * A(i) | |||
;Algorithm | ;Algorithm | ||
<math>O(n)</math> work and <math>O(\log n)</math> time | <math>O(n)</math> work and <math>O(\log n)</math> time | ||
<pre> | <pre> | ||
| Line 100: | Line 111: | ||
==Technique: Merge Sorting Cluster== | ==Technique: Merge Sorting Cluster== | ||
===Technique: Partitioning=== | ===Technique: Partitioning=== | ||
* Merging: Given two sorted arrays, A and B, create a sorted array C consisting of elements in A and B | |||
* Ranking: Given an element x, find <math>Rank(x, A) = i</math> defined such that <math>A(i) \leq x \leq A(i+1)</math> | *Merging: Given two sorted arrays, A and B, create a sorted array C consisting of elements in A and B | ||
** Note the book sometimes uses <math>Rank(i,B)</math> to denote <math>Rank(A(i), B)</math>. | *Ranking: Given an element x, find <math>Rank(x, A) = i</math> defined such that <math>A(i) \leq x \leq A(i+1)</math> | ||
**Note the book sometimes uses <math>Rank(i,B)</math> to denote <math>Rank(A(i), B)</math>. | |||
;Equivalence of Merging and Ranking | ;Equivalence of Merging and Ranking | ||
* Given an algorithm for merging, we know A(i) belongs in C(j) so Rank(A(i), B) = j-i | |||
* Given an algorithm for ranking, we get A(i) belongs in C(j) where j = Rank(A(i), B) + i | *Given an algorithm for merging, we know A(i) belongs in C(j) so Rank(A(i), B) = j-i | ||
*Given an algorithm for ranking, we get A(i) belongs in C(j) where j = Rank(A(i), B) + i | |||
;Naive algorithm | ;Naive algorithm | ||
Apply binary search element wise on concurrent read system. | Apply binary search element wise on concurrent read system. | ||
O(log n) time, O(nlog n) work | O(log n) time, O(nlog n) work | ||
| Line 118: | Line 132: | ||
;Partitioning paradigm | ;Partitioning paradigm | ||
Input size: n | Input size: n | ||
* Partition the input into p jobs of size approx. n/p | |||
* Do small jobs concurrently using a separate (possibly serial) algo for each. | *Partition the input into p jobs of size approx. n/p | ||
*Do small jobs concurrently using a separate (possibly serial) algo for each. | |||
Example: | Example: | ||
Total work O(n), total time O(log n) | Total work O(n), total time O(log n) | ||
| Line 137: | Line 154: | ||
;Notes | ;Notes | ||
* We do not need to compute A_end or B_end. Just continue merging until we hit some index where (i % x)=0 in A or B. | |||
*We do not need to compute A_end or B_end. Just continue merging until we hit some index where (i % x)=0 in A or B. | |||
===Techinque: Divide and Conquer=== | ===Techinque: Divide and Conquer=== | ||
;Merge Sort | ;Merge Sort | ||
Input: Array A[1..n]<br> | Input: Array A[1..n]<br> | ||
Complexity:<br> | Complexity:<br> | ||
| Line 160: | Line 179: | ||
===Technique: Accelerating Cascades=== | ===Technique: Accelerating Cascades=== | ||
Consider: for problem of size n, there are two parallel algorithms.<br> | Consider: for problem of size n, there are two parallel algorithms.<br> | ||
* Algo A: <math>W_1(n)</math> work, <math>T_1(n)</math> time | |||
* Algo B: Work <math>W_2(n) > W_1(n)</math>. Time <math>T_2(n) < T_1(n)</math>. Faster but less efficient. | *Algo A: <math>W_1(n)</math> work, <math>T_1(n)</math> time | ||
*Algo B: Work <math>W_2(n) > W_1(n)</math>. Time <math>T_2(n) < T_1(n)</math>. Faster but less efficient. | |||
Assume Algo A is a "reducing algorithm"<br> | Assume Algo A is a "reducing algorithm"<br> | ||
We start with Algo A until the size is below some threshold. Then we switch to Algo B. | We start with Algo A until the size is below some threshold. Then we switch to Algo B. | ||
E.g. | E.g. | ||
* Algo 1 runs in <math>O(\log n)</math> iterations each taking <math>O(\log n)</math> time and <math>O(n)</math> work. Each iteration reduces the size to (3/4)m. | |||
* Algo 2 runs in <math>O(\log n)</math> time and <math>O(n\log n)</math> work. | *Algo 1 runs in <math>O(\log n)</math> iterations each taking <math>O(\log n)</math> time and <math>O(n)</math> work. Each iteration reduces the size to (3/4)m. | ||
* Run Algo 1 for <math>O(\log \log n)</math> rounds then run algo 2. | *Algo 2 runs in <math>O(\log n)</math> time and <math>O(n\log n)</math> work. | ||
** Total time is <math>O(\log n \log \log n)</math> and work is <math>O(n)</math> | *Run Algo 1 for <math>O(\log \log n)</math> rounds then run algo 2. | ||
**Total time is <math>O(\log n \log \log n)</math> and work is <math>O(n)</math> | |||
===Problem: Selection=== | ===Problem: Selection=== | ||
;Algorithm 1 | ;Algorithm 1 | ||
* Partition elements into rows of <math>\log n</math> size | |||
* For each row, find the median within the row | *Partition elements into rows of <math>\log n</math> size | ||
* Find the median of medians (MoM) in <math>O(n)</math> | *For each row, find the median within the row | ||
* Put all rows with median <= MoM above and all rows with median >= Mom below | *Find the median of medians (MoM) in <math>O(n)</math> | ||
* Now <math>m/4</math> elements are smaller and <math>m/4</math> are larger | *Put all rows with median <= MoM above and all rows with median >= Mom below | ||
** Known as the reducing lemma | *Now <math>m/4</math> elements are smaller and <math>m/4</math> are larger | ||
**Known as the reducing lemma | |||
This algorithm solves the selection problem in <math>O(\log^2 n)</math> time and <math>O(n)</math> work. | This algorithm solves the selection problem in <math>O(\log^2 n)</math> time and <math>O(n)</math> work. | ||
; Accelerating Cascades | ;Accelerating Cascades | ||
* What we have: | |||
** Algorithm 1 has <math>O(\log n)</math> iterations. | *What we have: | ||
:: Each iteration reduces a size m instance in <math>O(\log m)</math> time and <math>O(m)</math> work to an instance of size <math>\leq 3m/4</math> | **Algorithm 1 has <math>O(\log n)</math> iterations. | ||
** Algorithm 2 runs in <math>O(\log n)</math> time and <math>O(n \log n)</math> work. | ::Each iteration reduces a size m instance in <math>O(\log m)</math> time and <math>O(m)</math> work to an instance of size <math>\leq 3m/4</math> | ||
* Step 1: Use algo 1 to reduce from n to <math>n / \log n</math> | **Algorithm 2 runs in <math>O(\log n)</math> time and <math>O(n \log n)</math> work. | ||
* Step 2: Apply algorithm 2 | |||
*Step 1: Use algo 1 to reduce from n to <math>n / \log n</math> | |||
*Step 2: Apply algorithm 2 | |||
Total time is <math>O(\log n \log\log n)</math> and total work is <math>O(n)</math> | |||
===Informal Work-Depth (IWD)=== | ===Informal Work-Depth (IWD)=== | ||
| Line 202: | Line 230: | ||
===Algorithm=== | ===Algorithm=== | ||
* Partition A into n/r subarrays <math>B_1,...,B_{n/r}</math> | |||
** Sort each subarray separately using serial bucket sort (counting sort) | *Partition A into n/r subarrays <math>B_1,...,B_{n/r}</math> | ||
** Compute number(v,s) # of elements of value v in <math>B_s</math> for <math>0\leq v \leq r-1</math> and <math>1 \leq s \leq n/r</math> | **Sort each subarray separately using serial bucket sort (counting sort) | ||
** Compute serial(i) = # of elements in the block <math>B_s</math> such that A(j)=A(i) and <math> j < i </math> <math>1 \leq j \neq n</math> | **Compute number(v,s) # of elements of value v in <math>B_s</math> for <math>0\leq v \leq r-1</math> and <math>1 \leq s \leq n/r</math> | ||
* Run prefix sum on number(v,1),number(v,2),...,number(v,n/r) into ps(v,1), ps(v,2),..., ps(v,n/r) | **Compute serial(i) = # of elements in the block <math>B_s</math> such that A(j)=A(i) and <math> j < i </math> <math>1 \leq j \neq n</math> | ||
* Compute prefix sums of cardinality(0),.., cardinality(r-1) into global_ps(0),...,global_ps(r-1) | *Run prefix sum on number(v,1),number(v,2),...,number(v,n/r) into ps(v,1), ps(v,2),..., ps(v,n/r) | ||
* The rank of element <math>i</math> is <math>1+serial(i)+ps(v,s-1)+global_ps(v-1)</math> | *Compute prefix sums of cardinality(0),.., cardinality(r-1) into global_ps(0),...,global_ps(r-1) | ||
*The rank of element <math>i</math> is <math>1+serial(i)+ps(v,s-1)+global_ps(v-1)</math> | |||
===Complexity=== | ===Complexity=== | ||
* Step 1:<math>T=O(r),\;W=O(r)</math> per subarray. | |||
** Total: <math>T=O(r),\; W=O(n)</math> | *Step 1:<math>T=O(r),\;W=O(r)</math> per subarray. | ||
* Step 2: <math>r</math> computations each <math>T=O(\log(n/r)),\; W=O(n/r)</math> | **Total: <math>T=O(r),\; W=O(n)</math> | ||
** Total <math>T=O(\log n),\; W=O(n)</math> | *Step 2: <math>r</math> computations each <math>T=O(\log(n/r)),\; W=O(n/r)</math> | ||
* Step 3: <math>T=O(\log r),\; W=O(r)</math> | **Total <math>T=O(\log n),\; W=O(n)</math> | ||
* Step 4: <math>T=O(1)\; W=O(n)</math> | *Step 3: <math>T=O(\log r),\; W=O(r)</math> | ||
* Total: <math>T=O(r + \log n),\; W=O(n)</math> | *Step 4: <math>T=O(1)\; W=O(n)</math> | ||
*Total: <math>T=O(r + \log n),\; W=O(n)</math> | |||
;Notes | ;Notes | ||
* Running time is not poly-log | |||
*Running time is not poly-log | |||
===Theorems=== | ===Theorems=== | ||
* The integer sorting algorithm runs in <math>O(r+\log n)</math> time and <math>O(n)</math> work | *The integer sorting algorithm runs in <math>O(r+\log n)</math> time and <math>O(n)</math> work | ||
* The integer sorting algorithm can be applied to run in time <math>O(k(r^{1/k}+\log n))</math> and work <math>O(kn)</math> | *The integer sorting algorithm can be applied to run in time <math>O(k(r^{1/k}+\log n))</math> and work <math>O(kn)</math> | ||
Radix sort using the basic integer sort (BIS) algorithm.<br> | Radix sort using the basic integer sort (BIS) algorithm.<br> | ||
If your range is 0 to n and and your radix is <math>\sqrt{n}</math> then you will need <math>log_{\sqrt{n}}(r) = 2</math> rounds. | If your range is 0 to n and and your radix is <math>\sqrt{n}</math> then you will need <math>\log_{\sqrt{n}}(r) = 2</math> rounds. | ||
==2-3 trees; Technique: Pipelining== | ==2-3 trees; Technique: Pipelining== | ||
| Line 236: | Line 267: | ||
===2-3 tree=== | ===2-3 tree=== | ||
A 2-3 tree is a rooted tree which has the properties: | A 2-3 tree is a rooted tree which has the properties: | ||
* Each node has 2-3 ordered children | |||
* For any internal node, every directed path to a leaf is the same length | *Each node has 2-3 ordered children | ||
*For any internal node, every directed path to a leaf is the same length | |||
Types of queries: | Types of queries: | ||
* ''search(a)'' | |||
* ''insert(a)'' | *''search(a)'' | ||
* ''delete(a)'' | *''insert(a)'' | ||
*''delete(a)'' | |||
====Serial Algorithms==== | ====Serial Algorithms==== | ||
* Deletion: discard(a) | |||
** Delete connection between a and parent of a | *Deletion: discard(a) | ||
** If parent has 1 child | **Delete connection between a and parent of a | ||
*** If parent's sibling has 2 children, move child to sibling and discard(parent) | **If parent has 1 child | ||
*** If parent's sibling has 3 children, take one child from sibling | ***If parent's sibling has 2 children, move child to sibling and discard(parent) | ||
***If parent's sibling has 3 children, take one child from sibling | |||
====Parallel Algorithms==== | ====Parallel Algorithms==== | ||
Assume concurrent read model | Assume concurrent read model | ||
* Insert: Suppose we want to insert sorted elements <math>c_1,...,c_k</math> into a tree with n elements. | |||
** Insert element <math>c_{k/2}</math>. | *Insert: Suppose we want to insert sorted elements <math>c_1,...,c_k</math> into a tree with n elements. | ||
** Then insert in parallel <math>(c_1,...,c_{k/2-1})</math> and <math>(c_{k/2+1},...,c_k)</math> | **Insert element <math>c_{k/2}</math>. | ||
** Time is <math>O(\log k \log n)</math> using <math>k</math> processors. | **Then insert in parallel <math>(c_1,...,c_{k/2-1})</math> and <math>(c_{k/2+1},...,c_k)</math> | ||
* Deletion: Suppose we want to delete sorted elements <math>c_1,...,c_k</math> | **Time is <math>O(\log k \log n)</math> using <math>k</math> processors. | ||
** Backwards Insertion | *Deletion: Suppose we want to delete sorted elements <math>c_1,...,c_k</math> | ||
** for t=0 to <math>\log k</math> | **Backwards Insertion | ||
*** if <math>i \equiv 2^t (\operatorname{mod}2^{t+1})</math> | **for t=0 to <math>\log k</math> | ||
**** discard(c_i) | ***if <math>i \equiv 2^t (\operatorname{mod}2^{t+1})</math> | ||
** Time is <math>O(\log n \log k)</math> without pipelining | ****discard(c_i) | ||
** With pipelining, complexity is <math>O(\log n + \log k)</math> | **Time is <math>O(\log n \log k)</math> without pipelining | ||
**With pipelining, complexity is <math>O(\log n + \log k)</math> | |||
===Pipelining=== | ===Pipelining=== | ||
* There are <math>\log k</math> waves of the absorb procedure. | |||
* Apply pipelining to make the time <math>O(\log n + \log k)</math> | *There are <math>\log k</math> waves of the absorb procedure. | ||
*Apply pipelining to make the time <math>O(\log n + \log k)</math> | |||
==Maximum Finding== | ==Maximum Finding== | ||
| Line 272: | Line 309: | ||
===Constant time, <math>O(n^2)</math> Work=== | ===Constant time, <math>O(n^2)</math> Work=== | ||
* Compare every pair of elements in A[1...n] | |||
*Compare every pair of elements in A[1...n] | |||
<pre> | <pre> | ||
for i=1 to n pardo | for i=1 to n pardo | ||
| Line 287: | Line 325: | ||
===<math>O(\log \log n)</math> time and <math>O(n\log \log n)</math> work algorithm=== | ===<math>O(\log \log n)</math> time and <math>O(n\log \log n)</math> work algorithm=== | ||
* Split A into <math>\sqrt{n}</math> subarrays | |||
* Find the max of each subarray recursively | *Split A into <math>\sqrt{n}</math> subarrays | ||
* Find the max of all subarrays in <math>O(n)</math> using the constant time algo | *Find the max of each subarray recursively | ||
*Find the max of all subarrays in <math>O(n)</math> using the constant time algo | |||
Complexity | Complexity | ||
* <math>T(n) \leq T(\sqrt{n}) + c_1</math> | |||
* <math>W(n) \leq \sqrt{n}W(\sqrt{n}) + c_2 n</math> | *<math>T(n) \leq T(\sqrt{n}) + c_1</math> | ||
* <math>T(n) = O(\log \log n)</math>, <math>W(n) = O(n\log \log n)</math> | *<math>W(n) \leq \sqrt{n}W(\sqrt{n}) + c_2 n</math> | ||
*<math>T(n) = O(\log \log n)</math>, <math>W(n) = O(n\log \log n)</math> | |||
===<math>O(\log \log n)</math> time and <math>O(n)</math> work=== | ===<math>O(\log \log n)</math> time and <math>O(n)</math> work=== | ||
* Step 1: Partition into blocks of size <math>\log \log n</math>. Then we have <math>n/ \log \log n</math> blocks. | *Step 1: Partition into blocks of size <math>\log \log n</math>. Then we have <math>n/ \log \log n</math> blocks. | ||
** Apply serial linear time algorithm to find maximum of each block | **Apply serial linear time algorithm to find maximum of each block | ||
** <math>O(\log \log n)</math> time and <math>O(n)</math> work. | **<math>O(\log \log n)</math> time and <math>O(n)</math> work. | ||
* Step 2: Apply doubly log algorithm to <math>n / \log \log n</math> maxima. | *Step 2: Apply doubly log algorithm to <math>n / \log \log n</math> maxima. | ||
** <math>O(\log \log n)</math> time and <math>O(n)</math> work. | **<math>O(\log \log n)</math> time and <math>O(n)</math> work. | ||
===Random Sampling=== | ===Random Sampling=== | ||
Maximum finding in <math>O(1)</math> time and <math>O(n)</math> work with very high probability | Maximum finding in <math>O(1)</math> time and <math>O(n)</math> work with very high probability | ||
* Step 1: Using aux array B of size <math>b^{7/8}</math>. Independently fill with random elements from A | *Step 1: Using aux array B of size <math>b^{7/8}</math>. Independently fill with random elements from A | ||
* Step 2: Find the max <math>m</math> in array B in <math>O(1)</math> time and <math>O(n)</math> work | *Step 2: Find the max <math>m</math> in array B in <math>O(1)</math> time and <math>O(n)</math> work | ||
** Last 3 pulses of the recursive doubly-log time algorithm: | **Last 3 pulses of the recursive doubly-log time algorithm: | ||
** Pulse 1: B is partitioned into <math>n^{3/4}</math> blocks of size <math>n^{1/8}</math> each. Find the max of each block. | **Pulse 1: B is partitioned into <math>n^{3/4}</math> blocks of size <math>n^{1/8}</math> each. Find the max of each block. | ||
** Pulse 2: <math>n^{3/4}</math> maxima are partitioned into <math>n^{1/2}</math> blocks of size <math>n^{1/4}</math> each. | **Pulse 2: <math>n^{3/4}</math> maxima are partitioned into <math>n^{1/2}</math> blocks of size <math>n^{1/4}</math> each. | ||
** Pulse 2: Find the max m of <math>n^{1/2}</math> maxima in <math>O(1)</math> time and <math>O(n)</math> work. | **Pulse 2: Find the max m of <math>n^{1/2}</math> maxima in <math>O(1)</math> time and <math>O(n)</math> work. | ||
* Step 3: While there is an element larger than m, throw the new element into an array of size <math>n^{7/8}</math>. | *Step 3: While there is an element larger than m, throw the new element into an array of size <math>n^{7/8}</math>. | ||
: Compute the maximum of the new array. | |||
:Compute the maximum of the new array. | |||
;Complexity | ;Complexity | ||
* Step 1 takes <math>O(1)</math> time and <math>O(n^{7/8})</math> work | |||
* Step 2 takes <math>O(1)</math> time and <math>O(n)</math> work | *Step 1 takes <math>O(1)</math> time and <math>O(n^{7/8})</math> work | ||
* Each time Step 3 takes <math>O(1)</math> time and <math>O(n)</math> work | *Step 2 takes <math>O(1)</math> time and <math>O(n)</math> work | ||
* With high probability, we only need one iteration (see theorem below) so the time is <math>O(1)</math> and work is <math>O(n^{7/8})</math> | *Each time Step 3 takes <math>O(1)</math> time and <math>O(n)</math> work | ||
*With high probability, we only need one iteration (see theorem below) so the time is <math>O(1)</math> and work is <math>O(n^{7/8})</math> | |||
====Theorem 8.2==== | ====Theorem 8.2==== | ||
| Line 327: | Line 369: | ||
The probability of not finishing in the above time is <math>O(1/n^c)</math>. | The probability of not finishing in the above time is <math>O(1/n^c)</math>. | ||
{{ hidden | Proof | | {{hidden | Proof | | ||
See page 58 of the classnotes.<br> | See page 58 of the classnotes.<br> | ||
| Line 340: | Line 382: | ||
;Inputs | ;Inputs | ||
* Vector of vertices which point to an index in edges | |||
* Vector of edges e.g. (1,2) | *Vector of vertices which point to an index in edges | ||
* Vector of pointers to identical edges e.g. index of (1,2) -> index of (2,1) | *Vector of edges e.g. (1,2) | ||
* A vertex <math>r</math> | *Vector of pointers to identical edges e.g. index of (1,2) -> index of (2,1) | ||
*A vertex <math>r</math> | |||
;Goal: | ;Goal: | ||
* Select a direction for each edge to make our graph a tree with root <math>r</math> | |||
*Select a direction for each edge to make our graph a tree with root <math>r</math> | |||
;Algorithm | ;Algorithm | ||
* Step 1: For every edge <math>(u,v)</math>, add two edges <math>u \rightarrow v</math> and <math>v \rightarrow u</math> | |||
* Step 2: For every directed edge <math>u \rightarrow v</math>, set a pointer to another directed edge from <math>v</math>, <math>next(u \rightarrow v)</math> | *Step 1: For every edge <math>(u,v)</math>, add two edges <math>u \rightarrow v</math> and <math>v \rightarrow u</math> | ||
** If our edge is 1 -> 2, then the next edge is the immediate next edge of edge 2->1 in our edges array | *Step 2: For every directed edge <math>u \rightarrow v</math>, set a pointer to another directed edge from <math>v</math>, <math>next(u \rightarrow v)</math> | ||
** If edge 2 -> 1 is the last edge coming out of 2, then the next edge is the first edge coming out of 2 | **If our edge is 1 -> 2, then the next edge is the immediate next edge of edge 2->1 in our edges array | ||
** Now we have an euler cycle (or euler tour) among the edges | **If edge 2 -> 1 is the last edge coming out of 2, then the next edge is the first edge coming out of 2 | ||
* Step 3: <math>next(u_{r,1} \rightarrow r) = NIL </math> | **Now we have an euler cycle (or euler tour) among the edges | ||
* Step 4: Apply a list ranking algorithm to the edges. | *Step 3: <math>next(u_{r,1} \rightarrow r) = NIL </math> | ||
* Step 5: Delete the edge between every two vertices with the lower ranking | ** The edge <math>u_{r,1} \rightarrow r</math> is the opposite edge of the first edge coming out of <math>r</math> | ||
*Step 4: Apply a list ranking algorithm to the edges. | |||
*Step 5: Delete the edge between every two vertices with the lower ranking | |||
;Notes | ;Notes | ||
* Every step except 4, list ranking, is a local operation which is constant time and linear work | |||
* Requires a list ranking algorithm | *Every step except 4, list ranking, is a local operation which is constant time and linear work | ||
*Requires a list ranking algorithm | |||
====Preorder Numbering==== | ====Preorder Numbering==== | ||
Define: tree-edges point away from root, non-tree edges point to root | Define: tree-edges point away from root, non-tree edges point to root | ||
* Step 1: For every edge pardo, if e is a tree edge, distance(e) = 1 else distance(e) = 0 | *Step 1: For every edge pardo, if e is a tree edge, distance(e) = 1 else distance(e) = 0 | ||
* Step 2: List ranking | *Step 2: List ranking | ||
* Step 3: For every edge e: u->v, preorder(v) = n-distance(e) + 1 | *Step 3: For every edge e: u->v, preorder(v) = n-distance(e) + 1 | ||
===Technique: Pointer Jumping=== | ===Technique: Pointer Jumping=== | ||
| Line 389: | Line 436: | ||
Correctness: <br> | Correctness: <br> | ||
* Each element will eventually point to the cashier | |||
* Distance will always be correct | *Each element will eventually point to the cashier | ||
** If next[i] = NIL then distance is to the cashier | *Distance will always be correct | ||
** Otherwise the distance is <math>2^k</math> | **If next[i] = NIL then distance is to the cashier | ||
**Otherwise the distance is <math>2^k</math> | |||
Complexity: <math>O(\log n)</math> time and <math>O(n\log n)</math> work | Complexity: <math>O(\log n)</math> time and <math>O(n\log n)</math> work | ||
===Work-optimal List Ranking=== | ===Work-optimal List Ranking=== | ||
; Complexity | *From our list A, pull a subset S with uniform density and sparcity | ||
*Remove S from A, creating a new subset <math>A-S</math>. | |||
* <math>O(log (n) log log (n)) time</math> | **For each element i in <math>S</math>, fix the next and distance of prev(i) | ||
**Run compaction | |||
*Recurse on <math>A-S</math> until size is <math>\leq n/\log n</math>. Then use pointer jumping. | |||
*Add <math>S</math> back to <math>A-S</math> | |||
;Complexity | |||
We get the same complexity for randomized and deterministic list ranking (see below)<br> | |||
Randomized has the complexity with high probability. | |||
*<math>O(\log (n) \log \log (n))</math> time | |||
*<math>O(n)</math> work | |||
Using a parallel prefix-sum algorith which runs in <math>O(\log n/\log \log n)</math> time, | |||
we can get list ranking in <math>O(\log n)</math> time and <math>O(n)</math> work. | |||
===Randomized Symmetry Breaking=== | ===Randomized Symmetry Breaking=== | ||
| Line 418: | Line 472: | ||
s(i) = 1 | s(i) = 1 | ||
</pre> | </pre> | ||
;Notes | |||
* The full randomized list ranking works in <math>O(\log n \log\log n)</math> time and <math>O(n)</math> work with high probability | |||
===Deterministic Symmetry Breaking=== | ===Deterministic Symmetry Breaking=== | ||
* Assign each element a unique tag, such as the index in the array | |||
* Convert the tag to binary. For each element i, tag(i)!=tag(next(i)). | *Assign each element a unique tag, such as the index in the array | ||
* Let k be the index of the rightmost bit (where 0 is the rightmost bit) differing between tag(i) and tag(next(i)) | *Convert the tag to binary. For each element i, tag(i)!=tag(next(i)). | ||
* Let b be the bit in tag(i) differing from tag(next(i)) | *Let k be the index of the rightmost bit (where 0 is the rightmost bit) differing between tag(i) and tag(next(i)) | ||
* Set the new tag to <code>(k<<1) + b</code> | *Let b be the bit in tag(i) differing from tag(next(i)) | ||
*Set the new tag to <code>(k<<1) + b</code> | |||
This algorithm takes <math>O(1)</math> time and <math>O(n)</math> work per iteration. | This algorithm takes <math>O(1)</math> time and <math>O(n)</math> work per iteration. | ||
| Line 433: | Line 491: | ||
===r-ruling set=== | ===r-ruling set=== | ||
An r-ruling set is a subset <math>S</math> of a linked list satisfying two properties: | An r-ruling set is a subset <math>S</math> of a linked list satisfying two properties: | ||
;Algorithm | *''Uniform Density'' If node <math>i</math> is not in S, then one of the <math>r</math> nodes following i will be in <math>S</math> | ||
*''Uniform Sparcity'' If node <math>i</math> is in <math>S</math> then node <math>next(i)</math> is not in <math>S</math> | |||
;Algorithm 1 | |||
The following algorithm gives us an r-ruling set with <math>r=2*\log n - 1</math> | The following algorithm gives us an r-ruling set with <math>r=2*\log n - 1</math> | ||
#Apply the deterministic coin tossing algorithm to give each element a tag in <math>[0,...,2*\log n - 1]</math> | |||
#For each element i in parallel, if i is a local maximum then add it to <math>S</math> | |||
;Optimal-Work 2-Ruling set | |||
<pre> | |||
Apply one iteration of deterministic coin tossing | |||
Sort elements by tags | |||
Initialize array S with 1s | |||
for k = 0 to 2*log(n)-1: | |||
for i such that tag(i) = k pardo | |||
if S(pre(i)) = S(next(i)) = 1: | |||
S(i) = 0 | |||
</pre> | |||
==Tree Contraction== | ==Tree Contraction== | ||
| Line 453: | Line 526: | ||
===Parallel Rake=== | ===Parallel Rake=== | ||
Rake all leaves such that: | Rake all leaves such that: | ||
* No two leaves have the same parent (stem) | |||
* The parent of a stem cannot be the stem of another leaf | *No two leaves have the same parent (stem) | ||
*The parent of a stem cannot be the stem of another leaf | |||
| Line 460: | Line 534: | ||
;Parallel Rake Contraction Scheme | ;Parallel Rake Contraction Scheme | ||
Apply legal parallel rakes until the tree becomes a 3-node binary tree | Apply legal parallel rakes until the tree becomes a 3-node binary tree | ||
;Parallel Rake Contraction Algorithm | ;Parallel Rake Contraction Algorithm | ||
Step 1 | ;Step 1 | ||
*Number leaves according to a DFS using the Euler tour algorithm.<br> | |||
Observation 3: | Observation 3: | ||
| Line 472: | Line 549: | ||
Proof: See the classnotes | Proof: See the classnotes | ||
Step 2: | ;Step 2: | ||
* Let <math>S_1</math> be nodes in <math>S</math> whose parents are not in <math>S</math>. | * Let <math>S_1</math> be nodes in <math>S</math> whose parents are not in <math>S</math>. | ||
* Let <math>L_1</math> be leaves in <math>L</math> whose parents are in <math>S_1</math>. | |||
* Apply parallel rakes to leaves in <math>L_1</math>, unless the parent is the root. | * Apply parallel rakes to leaves in <math>L_1</math>, unless the parent is the root. | ||
* Apply parallel rakes to leaves in <math>L - L_1</math>, unless the parent is the root. | * Apply parallel rakes to leaves in <math>L - L_1</math>, unless the parent is the root. | ||
| Line 491: | Line 569: | ||
The internal node will be <math>(a*l+b) \times (c*r+d)</math> where <math>\times</math> is either addition or multiplication.<br> | The internal node will be <math>(a*l+b) \times (c*r+d)</math> where <math>\times</math> is either addition or multiplication.<br> | ||
If we delete one leaf and it's parent (stem), we will modify these variables of the stem's parent. | If we delete one leaf and it's parent (stem), we will modify these variables of the stem's parent. | ||
===Tree Binarization=== | |||
;Note: This is not in the classnotes, but has been covered in exams. | |||
To apply the above techniques to general trees or k-ary trees, you should binarize your k-ary tree.<br> | |||
This is done as follows: | |||
* Suppose node <math>x</math> has <math>n > 2</math> children | |||
* Select one child to keep | |||
* Create a node <math>x'</math> | |||
* Move all <math>n-1</math> children to <math>x'</math> | |||
* Set child <math>x'</math> to be a child of <math>x</math> | |||
Complexity | |||
* The time is <math>O(max\_degree)</math> and the work is <math>O(n)</math> | |||
==Graph Connectivity== | ==Graph Connectivity== | ||
| Line 501: | Line 593: | ||
Definitions: | Definitions: | ||
* Pointer Graph | |||
* Supervertices | *Pointer Graph | ||
* The supervertex graph | *Supervertices | ||
* Hookings | *The supervertex graph | ||
* Parallel pointer jumping | *Hookings | ||
*Parallel pointer jumping | |||
===A first connectivity algorithm=== | ===A first connectivity algorithm=== | ||
The first connectivity algorithm consists of <math>\log(n)</math> iterations of the following two steps: | The first connectivity algorithm consists of <math>\log(n)</math> iterations of the following two steps: | ||
* Hookings - Each root hooks itself the the minimal adjacent root. If there are no adjacent stars, then this rooted star quits. | |||
* Parallel pointer jumping - Each vertex performs pointer jumping until every vertex points to the root, forming a rooted star. | *Hookings - Each root hooks itself the the minimal adjacent root. If there are no adjacent stars, then this rooted star quits. | ||
*Parallel pointer jumping - Each vertex performs pointer jumping until every vertex points to the root, forming a rooted star. | |||
;Theorems | ;Theorems | ||
# The pointer graph always consists of rooted trees. | |||
# After <math>\log n</math> iterations, all vertices are contained in rooted stars that quit. | #The pointer graph always consists of rooted trees. | ||
#: Each connected component is represented by a single rooted star. | #After <math>\log n</math> iterations, all vertices are contained in rooted stars that quit. | ||
#:Each connected component is represented by a single rooted star. | |||
;Complexity | ;Complexity | ||
* We need <math>O(\log n)</math> iterations | |||
** Hookings take <math>O(1)</math> time and <math>O(n+m)</math> work | *We need <math>O(\log n)</math> iterations | ||
** Pointer jumping takes <math>O(\log n)</math> time and <math>O(n\log n)</math> work | **Hookings take <math>O(1)</math> time and <math>O(n+m)</math> work | ||
* For adjacency matrix, in total we need <math>O(\log^2 n)</math> time and <math>O(n^2\log n)</math> work since we have a processor per <math>n^2</math> possible edges. | **Pointer jumping takes <math>O(\log n)</math> time and <math>O(n\log n)</math> work | ||
* For incidence lists, we need <math>O(\log^2 n)</math> time and <math>O(n\log^2 n + m\log n)</math> work since we have a processor per edge. | *For adjacency matrix, in total we need <math>O(\log^2 n)</math> time and <math>O(n^2\log n)</math> work since we have a processor per <math>n^2</math> possible edges. | ||
*For incidence lists, we need <math>O(\log^2 n)</math> time and <math>O(n\log^2 n + m\log n)</math> work since we have a processor per edge. | |||
===A second connectivity algorithm=== | ===A second connectivity algorithm=== | ||
| Line 530: | Line 626: | ||
Each iteration takes constant time. | Each iteration takes constant time. | ||
# Probe quitting: each rooted star whose supervertex is not adjacent to any other quits | #Probe quitting: each rooted star whose supervertex is not adjacent to any other quits | ||
# Hooking on smaller: each rooted star hooks onto a smaller vertex of another supervertex which is not a leaf | #Hooking on smaller: each rooted star hooks onto a smaller vertex of another supervertex which is not a leaf | ||
#* Note that this is not unique. Requires arbitrary CRCW. | #*Note that this is not unique. Requires arbitrary CRCW. | ||
# Hooking non-hooked-upon: every rooted star not hooked upon in step 2 hooks to another vertex in another supervertex which is not a leaf | #Hooking non-hooked-upon: every rooted star not hooked upon in step 2 hooks to another vertex in another supervertex which is not a leaf | ||
# Parallel pointer jumping: one round of parallel pointer jumping | #Parallel pointer jumping: one round of parallel pointer jumping | ||
;Theorems | ;Theorems | ||
*The pointer graph always consists of rooted trees. | |||
*For every vertex which is not a leaf, <math>D(v) \leq v</math> | |||
{{hidden | Proof | | |||
* This is true after steps 1, 2, and 4. | |||
** This follows immediately for 1 and 2. | |||
** After one round of pointer jumping (4) after 3, everyone from supervertex <math>r</math> is a leaf due to the claim below. | |||
* Consider a root <math>r</math> which hooks on someone larger in step 3. | |||
*: After Step 3, all children of <math>r</math> are leaves. | |||
*: I.e. no one else will hook to <math>r</math> during Step 3. | |||
** If anyone was larger, <math>r</math> would have hooked on them in Step 2. | |||
** If anyone was smaller, they would have hooked on <math>r</math> in Step 2. | |||
}} | |||
;Complexity | ;Complexity | ||
*Time <math>O(\log n)</math> | |||
*Work <math>O((n+m)\log n)</math> | |||
;Notes | |||
*Without step 3, the algorithm will run in <math>O(n)</math> time instead of <math>O(\log n)</math> but the result will be valid. | |||
*In step 2, you can hook rooted trees in addition to rooted stars for better empirical performance | |||
{{hidden | Proof | | |||
Let <math>h(T)</math> be the height of tree T where a two-layer tree has height 1.<br> | |||
Define a single node to have height 1.<br> | |||
Let <math>H</math> be the sum of heights of all trees and <math>\bar{H}</math> be the total height after one iteration. | |||
* Claim: <math>\bar{H} \leq 2*H/3</math> | |||
}} | |||
===Minimum Spanning Forest=== | ===Minimum Spanning Forest=== | ||
====The MSF Theorem==== | |||
Let <math>G(V,E)</math> be a weighted graph and let <math>U</math> and <math>V-U</math> be two non-empty subsets of <math>V</math>. | |||
Consider set <math>H=\{(u,v) \mid u \in U, v \in V\}</math> of edges connecting points in <math>U</math> and <math>V</math>. | |||
If <math>e</math> is the edge of minimum weight in <math>H</math>, then <math>e</math> is in the MSF of <math>G</math> | |||
====A first MSF algorithm==== | |||
* Sort the edges by weight. Assign a processor to each edge. Using a priority CRCW, the edge with minimum weight will take priority during writes. | |||
Each round consists of hooking and <math>\log n</math> rounds of parallel pointer jumping | |||
* Each root find the minimum weight edge to another supervertex and hooks itself to that root. | |||
*: This is automatic from the priority CRCW. | |||
====A second MSF algorithm==== | |||
We replace steps 2 and 3 in the connectivity algorithm with the simple rule: | |||
* We hook rooted stars using the edge with the smallest weight. | |||
;Notes | |||
* The progression of edge weights up the tree are monotonically increasing so there are no cycles | |||
===Biconnectivity=== | |||
This section is not it the textbook. It is from Tarjan and Vishkin (1985)<ref name="tarjan1985biconnectivity">Robert E. Tarjan, and Uzi Vishkin. ''An Efficient Parallel Biconnectivity Algorithm'' (1985). SIAM Journal on Computing. DOI: [https://doi.org/10.1137/0214061 10.1137/0214061] [https://epubs.siam.org/doi/10.1137/0214061 https://epubs.siam.org/doi/10.1137/0214061] [https://www.researchgate.net/publication/220617428_An_Efficient_Parallel_Biconnectivity_Algorithm Mirror]</ref>. | |||
A graph is biconnected if for every two vertices <math>v_1</math> and <math>v_2</math>, there is a simple cycle containing <math>v_1</math> and <math>v_2</math>. | |||
Intuitively this means that for any two vertices, there are at least two paths from <math>v_1</math> to <math>v_2</math>. If any vertex and its edges are removed from a biconnected graph, it still remains connected. | |||
Every connected graph consists of biconnected components. These are sets of edges such that every two edges from a set lie on a simple cycle. | |||
Vertices which connect two biconnected components are called ''articulation points''. | |||
If these points are removed, the two biconnected components are no longer connected. | |||
;Algorithm | |||
Assume we are given a connected graph <math>G</math>. | |||
# First build a spanning tree <math>T</math>. Record which edges are in the spanning tree. Root the spanning tree. | |||
# Compute the preorder number of all edges using an euler tour. | |||
# For every vertex <math>v</math>, calculate the hi and low preorder numbers in the subtree <math>T(v)</math> | |||
# Create the auxiliary graph <math>G'' = (V'', E'')</math> as follows: | |||
#* All edges of <math>G</math> are vertices in <math>G''</math> | |||
#* For each edge <math>(v, w)</math> in <math>G - T</math>, add edge <math> ((p(v),v),(p(w),w))</math> to <math>G''</math> iff <math>v</math> and <math>w</math> are unrelated in <math>T</math> | |||
#* For each edge <math>(v = p(w), w)</math> in <math>T</math>, add edge <math>((p(v), v), (v, w))</math> to <math>G''</math> iff <math>low(w) < v</math> or <math>high(w) \geq v + size(v)</math> | |||
# Compute the connected components of <math>G''</math> | |||
# Assign edges based on their connected components. | |||
;Complexity | |||
* <math>O(\log n)</math> time | |||
==Tricks== | |||
===Removing duplicates in an array=== | |||
Assume you have an Arbitrary CRCW | |||
# Given array A of size n with entries 0 to n-1 | |||
# For each entry pardo | |||
#* Write B[A[i]] == i | |||
#* Only one write will succeed for each unique A[i] | |||
#* Check if B[A[i]] == i | |||
===Compaction of an <math>n^2</math> array with <math>\leq n</math> elements in <math>O(\log n)</math> time=== | |||
* Split our <math>n^2</math> array to n subarrays, each of size <math>n</math> | |||
* Run <math>n</math> parallel compactions on each subarray | |||
* Perform one compaction on the size of each subarray | |||
* Compact all elements using (total size of prev subarrays + position in current subarray) | |||
The benefit of this segmented compaction/prefix sum is that if you only do each segment once in an iterative algorithm such as parallel BFS, | |||
you can get <math>O(n^2)</math> or <math>O(m)</math> work. | |||
==XMT Programming Tips== | |||
I never figured out how to use standard c headers. | |||
* XMT only has int (32 bit) and float (32 bit). If you need a bool type, you will need to define it in a header. | |||
* You cannot call functions from within <code>spawn</code> | |||
Here is my helpers header <code>helpers.h</code> | |||
{{ hidden | <code>helpers.h</code> | | |||
<syntaxhighlight lang="c"> | |||
#ifndef HELPERS_H | |||
#define HELPERS_H | |||
#define true 1 | |||
#define false 0 | |||
#define bool int | |||
// #define NIL -1 | |||
#define max(a, b) ((((a) < (b)) ? (b) : (a))) | |||
#define min(a, b) ((((a) < (b)) ? (a) : (b))) | |||
#endif | |||
</syntaxhighlight> | |||
}} | |||
If you prefer to debug in C++ like me, you can use the following code to adapt running the XMT code: | |||
This code does not run things asynchronously. | |||
{{hidden | C++ Code | | |||
<syntaxhighlight lang="cpp"> | |||
#define spawn(x, y) for (int $ = x; $ <= y; ++$) | |||
//#define spawn(x, y) for (int $ = y; $ >= x; --$) | |||
#define ps(a, b) \ | |||
{ \ | |||
b += a; \ | |||
a = b - a; \ | |||
} | |||
#define psm(a, b) \ | |||
{ \ | |||
b += a; \ | |||
a = b - a; \ | |||
} | |||
#define psBaseReg int | |||
#define STRINGIFY2(X) #X | |||
#define STRINGIFY(X) STRINGIFY2(X) | |||
using namespace std; | |||
#define GRAPH_NUM graph0 | |||
#define N 19 | |||
#define M 36 | |||
vector<int> vertices; | |||
vector<int> degrees; | |||
vector<vector<int>> edges; | |||
int main() { | |||
vertices.resize(N); | |||
degrees.resize(N); | |||
edges = std::vector<std::vector<int>>(M, std::vector<int>(2)); | |||
string datapath = "data/" STRINGIFY(GRAPH_NUM) "/graph.txt"; | |||
string data = readFile(datapath); | |||
regex section_regex( | |||
"[\\n\\r][\\n\\r]+|[\\r\\n]0\\s[\\r\\n]+", | |||
std::regex_constants::ECMAScript | std::regex_constants::icase); | |||
regex space_regex("[\\n\\s\\r]+", std::regex_constants::ECMAScript | | |||
std::regex_constants::icase); | |||
vector<string> sections = split(data, section_regex); | |||
// for (int i = 0; i < sections.size(); i++) { | |||
// cout << "Section " << i << " " << sections[i].size() << endl; | |||
// cout << sections[i] << endl; | |||
//} | |||
return 0; | |||
} | |||
string readFile(const string& datapath) { | |||
std::ifstream in(datapath, std::ios::in); | |||
string data; | |||
if (in.good()) { | |||
std::string contents; | |||
in.seekg(0, std::ios::end); | |||
contents.resize(static_cast<unsigned int>(in.tellg())); | |||
in.seekg(0, std::ios::beg); | |||
in.read(&contents[0], contents.size()); | |||
return contents; | |||
} | |||
std::cerr << "Failed to open file: " << datapath << std::endl; | |||
throw(errno); | |||
} | |||
vector<string> split(string s, regex r) { | |||
vector<string> splits; | |||
smatch m; // <-- need a match object | |||
while (regex_search(s, m, r)) // <-- use it here to get the match | |||
{ | |||
int split_on = m.position(); // <-- use the match position | |||
splits.push_back(s.substr(0, split_on)); | |||
s = s.substr(split_on + m.length()); // <-- also, skip the whole match | |||
} | |||
if (!s.empty()) { | |||
splits.push_back(s); // and there may be one last token at the end | |||
} | |||
return splits; | |||
} | |||
</syntaxhighlight> | |||
}} | |||
==Hardware/Architecture== | ==Hardware/Architecture== | ||
| Line 548: | Line 850: | ||
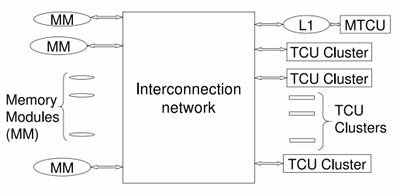
[[File:Pram hardware diagram.jpg | 400px]] | [[File:Pram hardware diagram.jpg | 400px]] | ||
* MTCU - Master Thread Control Unit - runs in serial mode | *MTCU - Master Thread Control Unit - runs in serial mode | ||
* TCU Cluster - Thread Control Unit | *TCU Cluster - Thread Control Unit | ||
;Procedure | ;Procedure | ||
* Spawn broadcasts your spawn code in the block to every thread control unit (TCU). | |||
* Data is shared through the interconnection network | *Spawn broadcasts your spawn code in the block to every thread control unit (TCU). | ||
*Data is shared through the interconnection network | |||
;Performance Penalty | ;Performance Penalty | ||
<math>\text{Execution Depth} = \text{Computation Depth} + LSRTM \times R + QD</math> | <math>\text{Execution Depth} = \text{Computation Depth} + LSRTM \times R + QD</math> | ||
* <math>LSTRM</math> - length of sequence of round trips to memory | |||
* <math>R</math> - time for round trip to memory | *<math>LSTRM</math> - length of sequence of round trips to memory | ||
* <math>QD</math> - queuing delay | *<math>R</math> - time for round trip to memory | ||
** If multiple threads access the same memory module, they are queued at the memory module | *<math>QD</math> - queuing delay | ||
**If multiple threads access the same memory module, they are queued at the memory module | |||
==Resources== | ==Resources== | ||
* [https://stanford.edu/~rezab/dao/ Stanford CME323 Distributed Algorithms Lectures 1-3] | |||
*[https://stanford.edu/~rezab/dao/ Stanford CME323 Distributed Algorithms Lectures 1-3] | |||
===Textbooks=== | ===Textbooks=== | ||
== | *[http://users.umiacs.umd.edu/~vishkin/PUBLICATIONS/classnotes.pdf Uzi Vishkin ENEE651/CMSC751 Classnotes] | ||
[ | *[https://www.amazon.com/Introduction-Parallel-Algorithms-Joseph-JaJa/dp/0201548569?sa-no-redirect=1&pldnSite=1 Introduction to Parallel Algorithms (Joseph Jaja, textbook)] | ||
*[https://www.cs.cmu.edu/~guyb/papers/BM04.pdf Parallel Algorithms by Guy E. Blelloch and Bruce M. Maggs (CMU)] | |||
==References== | |||
Latest revision as of 16:21, 13 May 2022
Parallel Algorithms notes from CMSC751 with Uzi Vishkin.
This class is based on his book Thinking in Parallel Some Basic Data-Parallel Algorithms and Techniques
Class Website
XMT Language
XMTC is a single-program multiple-data (SPMD) extension of C.
- Spawn creates threads
- Threads expire at Join
$represents the number of the threadPS Ri Rjis an atomic prefix sum- Stores Ri + Rj in Ri
- Stores the original value of Ri in Rj
int x = 0;
// Spawn n threads
spawn(0, n-1) {
int e = 1;
if (A[$] != 0) {
// Sets e=x and increments x
ps(e,x);
}
}
Models
PRAM
Parallel Random-Access Machine/Model
You're given n synchronous processors each with local memory and access to a shared memory.
Each processor can write to shared memory, read to shared memory, or do computation in local memory.
You tell each processor what to do at each time step.
Types of PRAM
- exclusive-read exclusive-write (EREW)
- concurrent-read exclusive-write (CREW)
- concurrent-read concurrent-write (CRCW)
- Arbitrary CRCW - an arbitrary processor writing succeeds
- Priority CRCW - the lowest numbered processor writing succeeds
- Common CRCW - writing succeeds only if all processors write the same value
Drawbacks
- Does not reveal how the algorithm will run on PRAMs with different number of proc
- Fully specifying allocation requires an unnecessary level of detail
Work Depth
You provide a sequence of instructions. At each time step, you specify the number of parallel operations.
WD-presentation Sufficiency Theorem
Given an algorithm in WD mode that takes \(\displaystyle x=x(n)\) operations and \(\displaystyle d=d(n)\) time, the algorithm can be implemented in any p-processor PRAM with \(\displaystyle O(x/p + d)\) time.
- Notes
- Other resources call this Brent's theorem
- \(\displaystyle x\) is the work and \(\displaystyle d\) is the depth
Speedup
- A parallel algorithm is work-optimal if W(n) grows asymptotically the same as T(n).
- A work-optimal parallel algorithm is work-time-optimal if T(n) cannot be improved by another work-optimal algorithm.
- If T(n) is best known and W(n) matches it, this is called linear-speedup
NC Theory
Nick's Class Theory
- Good serial algorithms: Poly time
- Good parallel algorithm: poly-log \(\displaystyle O(\log ^c n)\) time, poly processors
Technique: Balanced Binary Trees
Example Applications:
- Prefix sum
- Largest element
- Nearest-one element
- Compaction
- Inputs
- Array A[1..n] of elements
- Associative binary operation, denoted * (e.g. addition, multiplication, min, max)
- Outputs
- Array B containing B(i) = A(1) * ... * A(i)
- Algorithm
\(\displaystyle O(n)\) work and \(\displaystyle O(\log n)\) time
for i, 1 <= i <= n pardo
B(0, i) = A(i)
// Summation step up the tree
for h=1 to log n
B(h, i) = B(h-1, 2i-1) * B(h-1, 2i)
// Down the tree
for h=log n to 1
if i even, i <= n/2^h
C(h, i) = C(h+1, i/2)
if i == 1
C(h, i) = B(h, i)
if i odd, 3 <= i <= n/2^h
C(h, i) = C(h+1, i/2) * B(h, i)
return C(0, :)
Technique: Merge Sorting Cluster
Technique: Partitioning
- Merging: Given two sorted arrays, A and B, create a sorted array C consisting of elements in A and B
- Ranking: Given an element x, find \(\displaystyle Rank(x, A) = i\) defined such that \(\displaystyle A(i) \leq x \leq A(i+1)\)
- Note the book sometimes uses \(\displaystyle Rank(i,B)\) to denote \(\displaystyle Rank(A(i), B)\).
- Equivalence of Merging and Ranking
- Given an algorithm for merging, we know A(i) belongs in C(j) so Rank(A(i), B) = j-i
- Given an algorithm for ranking, we get A(i) belongs in C(j) where j = Rank(A(i), B) + i
- Naive algorithm
Apply binary search element wise on concurrent read system. O(log n) time, O(nlog n) work
for 1 <= i <= n pardo Rank(A(i), B) Rank(B(i), A)
- Partitioning paradigm
Input size: n
- Partition the input into p jobs of size approx. n/p
- Do small jobs concurrently using a separate (possibly serial) algo for each.
Example: Total work O(n), total time O(log n)
// Partitioning for 1 <= i <= p pardo b(i) = Rank((n/p)(i-1)+1, B) a(i) = Rank((n/p)(i-1)+1, A) // Total slice size is <= 2n/p. Total 2p slices. // E.g. slice size is 2 * log(n) if p=n/log(n). // Work for 1 <= i <= p pardo k = ceil(b(i)/(n/p)) * (n/p) merge slice A[(n/p)(i-1)+1:min(a(i), end_a] and B[b(i):end_b]
- Notes
- We do not need to compute A_end or B_end. Just continue merging until we hit some index where (i % x)=0 in A or B.
Techinque: Divide and Conquer
- Merge Sort
Input: Array A[1..n]
Complexity:
Time: \(\displaystyle T(n) \leq T(n/2) + \alpha \log n\)
Work: \(\displaystyle T(n) \leq 2 * T(n/2) + \beta n\)
Time \(\displaystyle O(\log^2 n)\). Work: \(\displaystyle O(n \log n)\)
MergeSort(A, B):
if n == 1
return B(1) = A(1)
call in parallel:
MergeSort(A[1:n/2], C[1:n/2])
MergeSort(A[n/2+1:n], C[n/2+1:n])
Merge C[1:n/2] and C[n/2:n] using O(log n) algorithm
Technique: Informal Work-Depth (IWD) and Accelerating Cascades
Technique: Accelerating Cascades
Consider: for problem of size n, there are two parallel algorithms.
- Algo A: \(\displaystyle W_1(n)\) work, \(\displaystyle T_1(n)\) time
- Algo B: Work \(\displaystyle W_2(n) \gt W_1(n)\). Time \(\displaystyle T_2(n) \lt T_1(n)\). Faster but less efficient.
Assume Algo A is a "reducing algorithm"
We start with Algo A until the size is below some threshold. Then we switch to Algo B.
E.g.
- Algo 1 runs in \(\displaystyle O(\log n)\) iterations each taking \(\displaystyle O(\log n)\) time and \(\displaystyle O(n)\) work. Each iteration reduces the size to (3/4)m.
- Algo 2 runs in \(\displaystyle O(\log n)\) time and \(\displaystyle O(n\log n)\) work.
- Run Algo 1 for \(\displaystyle O(\log \log n)\) rounds then run algo 2.
- Total time is \(\displaystyle O(\log n \log \log n)\) and work is \(\displaystyle O(n)\)
Problem: Selection
- Algorithm 1
- Partition elements into rows of \(\displaystyle \log n\) size
- For each row, find the median within the row
- Find the median of medians (MoM) in \(\displaystyle O(n)\)
- Put all rows with median <= MoM above and all rows with median >= Mom below
- Now \(\displaystyle m/4\) elements are smaller and \(\displaystyle m/4\) are larger
- Known as the reducing lemma
This algorithm solves the selection problem in \(\displaystyle O(\log^2 n)\) time and \(\displaystyle O(n)\) work.
- Accelerating Cascades
- What we have:
- Algorithm 1 has \(\displaystyle O(\log n)\) iterations.
- Each iteration reduces a size m instance in \(\displaystyle O(\log m)\) time and \(\displaystyle O(m)\) work to an instance of size \(\displaystyle \leq 3m/4\)
- Algorithm 2 runs in \(\displaystyle O(\log n)\) time and \(\displaystyle O(n \log n)\) work.
- Step 1: Use algo 1 to reduce from n to \(\displaystyle n / \log n\)
- Step 2: Apply algorithm 2
Total time is \(\displaystyle O(\log n \log\log n)\) and total work is \(\displaystyle O(n)\)
Informal Work-Depth (IWD)
At each time unit there is a set containing a number of instructions to be performed concurrently.
Integer Sorting
There is a theorem that sorting with only comparisons is worst case at least \(\displaystyle O(n\log n)\)
Input: Array A[1..n], integers are range [0..r-1]
Sorting: rank from smallest to largest
Assume n is divisible by r (\(\displaystyle r=\sqrt{n}\))
Algorithm
- Partition A into n/r subarrays \(\displaystyle B_1,...,B_{n/r}\)
- Sort each subarray separately using serial bucket sort (counting sort)
- Compute number(v,s) # of elements of value v in \(\displaystyle B_s\) for \(\displaystyle 0\leq v \leq r-1\) and \(\displaystyle 1 \leq s \leq n/r\)
- Compute serial(i) = # of elements in the block \(\displaystyle B_s\) such that A(j)=A(i) and \(\displaystyle j \lt i \) \(\displaystyle 1 \leq j \neq n\)
- Run prefix sum on number(v,1),number(v,2),...,number(v,n/r) into ps(v,1), ps(v,2),..., ps(v,n/r)
- Compute prefix sums of cardinality(0),.., cardinality(r-1) into global_ps(0),...,global_ps(r-1)
- The rank of element \(\displaystyle i\) is \(\displaystyle 1+serial(i)+ps(v,s-1)+global_ps(v-1)\)
Complexity
- Step 1:\(\displaystyle T=O(r),\;W=O(r)\) per subarray.
- Total: \(\displaystyle T=O(r),\; W=O(n)\)
- Step 2: \(\displaystyle r\) computations each \(\displaystyle T=O(\log(n/r)),\; W=O(n/r)\)
- Total \(\displaystyle T=O(\log n),\; W=O(n)\)
- Step 3: \(\displaystyle T=O(\log r),\; W=O(r)\)
- Step 4: \(\displaystyle T=O(1)\; W=O(n)\)
- Total: \(\displaystyle T=O(r + \log n),\; W=O(n)\)
- Notes
- Running time is not poly-log
Theorems
- The integer sorting algorithm runs in \(\displaystyle O(r+\log n)\) time and \(\displaystyle O(n)\) work
- The integer sorting algorithm can be applied to run in time \(\displaystyle O(k(r^{1/k}+\log n))\) and work \(\displaystyle O(kn)\)
Radix sort using the basic integer sort (BIS) algorithm.
If your range is 0 to n and and your radix is \(\displaystyle \sqrt{n}\) then you will need \(\displaystyle \log_{\sqrt{n}}(r) = 2\) rounds.
2-3 trees; Technique: Pipelining
Dictionary: Search, insert, delete
Problem: How to parallelize to handle batches of queries
2-3 tree
A 2-3 tree is a rooted tree which has the properties:
- Each node has 2-3 ordered children
- For any internal node, every directed path to a leaf is the same length
Types of queries:
- search(a)
- insert(a)
- delete(a)
Serial Algorithms
- Deletion: discard(a)
- Delete connection between a and parent of a
- If parent has 1 child
- If parent's sibling has 2 children, move child to sibling and discard(parent)
- If parent's sibling has 3 children, take one child from sibling
Parallel Algorithms
Assume concurrent read model
- Insert: Suppose we want to insert sorted elements \(\displaystyle c_1,...,c_k\) into a tree with n elements.
- Insert element \(\displaystyle c_{k/2}\).
- Then insert in parallel \(\displaystyle (c_1,...,c_{k/2-1})\) and \(\displaystyle (c_{k/2+1},...,c_k)\)
- Time is \(\displaystyle O(\log k \log n)\) using \(\displaystyle k\) processors.
- Deletion: Suppose we want to delete sorted elements \(\displaystyle c_1,...,c_k\)
- Backwards Insertion
- for t=0 to \(\displaystyle \log k\)
- if \(\displaystyle i \equiv 2^t (\operatorname{mod}2^{t+1})\)
- discard(c_i)
- if \(\displaystyle i \equiv 2^t (\operatorname{mod}2^{t+1})\)
- Time is \(\displaystyle O(\log n \log k)\) without pipelining
- With pipelining, complexity is \(\displaystyle O(\log n + \log k)\)
Pipelining
- There are \(\displaystyle \log k\) waves of the absorb procedure.
- Apply pipelining to make the time \(\displaystyle O(\log n + \log k)\)
Maximum Finding
Given an array A=A(1),...,A(n), find the largest element in the array
Constant time, \(\displaystyle O(n^2)\) Work
- Compare every pair of elements in A[1...n]
for i=1 to n pardo
B(i) = 0
for 1 <= i,j <= n pardo
if A(i) <= A(j) and i < j
B(i) = 1
else
B(j) = 1
for 1 <= i <= n pardo
if B(i) == 0
A(i) is the max
\(\displaystyle O(\log \log n)\) time and \(\displaystyle O(n\log \log n)\) work algorithm
- Split A into \(\displaystyle \sqrt{n}\) subarrays
- Find the max of each subarray recursively
- Find the max of all subarrays in \(\displaystyle O(n)\) using the constant time algo
Complexity
- \(\displaystyle T(n) \leq T(\sqrt{n}) + c_1\)
- \(\displaystyle W(n) \leq \sqrt{n}W(\sqrt{n}) + c_2 n\)
- \(\displaystyle T(n) = O(\log \log n)\), \(\displaystyle W(n) = O(n\log \log n)\)
\(\displaystyle O(\log \log n)\) time and \(\displaystyle O(n)\) work
- Step 1: Partition into blocks of size \(\displaystyle \log \log n\). Then we have \(\displaystyle n/ \log \log n\) blocks.
- Apply serial linear time algorithm to find maximum of each block
- \(\displaystyle O(\log \log n)\) time and \(\displaystyle O(n)\) work.
- Step 2: Apply doubly log algorithm to \(\displaystyle n / \log \log n\) maxima.
- \(\displaystyle O(\log \log n)\) time and \(\displaystyle O(n)\) work.
Random Sampling
Maximum finding in \(\displaystyle O(1)\) time and \(\displaystyle O(n)\) work with very high probability
- Step 1: Using aux array B of size \(\displaystyle b^{7/8}\). Independently fill with random elements from A
- Step 2: Find the max \(\displaystyle m\) in array B in \(\displaystyle O(1)\) time and \(\displaystyle O(n)\) work
- Last 3 pulses of the recursive doubly-log time algorithm:
- Pulse 1: B is partitioned into \(\displaystyle n^{3/4}\) blocks of size \(\displaystyle n^{1/8}\) each. Find the max of each block.
- Pulse 2: \(\displaystyle n^{3/4}\) maxima are partitioned into \(\displaystyle n^{1/2}\) blocks of size \(\displaystyle n^{1/4}\) each.
- Pulse 2: Find the max m of \(\displaystyle n^{1/2}\) maxima in \(\displaystyle O(1)\) time and \(\displaystyle O(n)\) work.
- Step 3: While there is an element larger than m, throw the new element into an array of size \(\displaystyle n^{7/8}\).
- Compute the maximum of the new array.
- Complexity
- Step 1 takes \(\displaystyle O(1)\) time and \(\displaystyle O(n^{7/8})\) work
- Step 2 takes \(\displaystyle O(1)\) time and \(\displaystyle O(n)\) work
- Each time Step 3 takes \(\displaystyle O(1)\) time and \(\displaystyle O(n)\) work
- With high probability, we only need one iteration (see theorem below) so the time is \(\displaystyle O(1)\) and work is \(\displaystyle O(n^{7/8})\)
Theorem 8.2
The algorithm find the maximum among \(\displaystyle n\) elements. With high probability it runs in \(\displaystyle O(1)\) time and \(\displaystyle O(n)\) work. The probability of not finishing in the above time is \(\displaystyle O(1/n^c)\).
See page 58 of the classnotes.
List Ranking Cluster
Techniques: Euler tours, pointer jumping, randomized and deterministic symmetry breaking
Rooting a tree
Technique: Euler tours
- Inputs
- Vector of vertices which point to an index in edges
- Vector of edges e.g. (1,2)
- Vector of pointers to identical edges e.g. index of (1,2) -> index of (2,1)
- A vertex \(\displaystyle r\)
- Goal
- Select a direction for each edge to make our graph a tree with root \(\displaystyle r\)
- Algorithm
- Step 1: For every edge \(\displaystyle (u,v)\), add two edges \(\displaystyle u \rightarrow v\) and \(\displaystyle v \rightarrow u\)
- Step 2: For every directed edge \(\displaystyle u \rightarrow v\), set a pointer to another directed edge from \(\displaystyle v\), \(\displaystyle next(u \rightarrow v)\)
- If our edge is 1 -> 2, then the next edge is the immediate next edge of edge 2->1 in our edges array
- If edge 2 -> 1 is the last edge coming out of 2, then the next edge is the first edge coming out of 2
- Now we have an euler cycle (or euler tour) among the edges
- Step 3: \(\displaystyle next(u_{r,1} \rightarrow r) = NIL \)
- The edge \(\displaystyle u_{r,1} \rightarrow r\) is the opposite edge of the first edge coming out of \(\displaystyle r\)
- Step 4: Apply a list ranking algorithm to the edges.
- Step 5: Delete the edge between every two vertices with the lower ranking
- Notes
- Every step except 4, list ranking, is a local operation which is constant time and linear work
- Requires a list ranking algorithm
Preorder Numbering
Define: tree-edges point away from root, non-tree edges point to root
- Step 1: For every edge pardo, if e is a tree edge, distance(e) = 1 else distance(e) = 0
- Step 2: List ranking
- Step 3: For every edge e: u->v, preorder(v) = n-distance(e) + 1
Technique: Pointer Jumping
List Ranking
Input: A dense array A. For each element except first, we have a node pointing its successor in the array.
Each element, except last, is the successor of one element.
rank(i)=0 for last, rank(i) = rank(next(i)) + 1 for the rest
The last element we call the "cashier".
Idea:
At iteration 0, node i points to node i+1
At iteration 1, node i points to node i+2
At iteration 2, node i points to node i+4...
for i 1 <= i <= n pardo:
if next[i] == NIL then distance[i] = 0 else distance[i] = 1
for k = 1 to log g:
distance[i] = distance[i] + distance[next[i]]
next[i] = next[next[i]]
Correctness:
- Each element will eventually point to the cashier
- Distance will always be correct
- If next[i] = NIL then distance is to the cashier
- Otherwise the distance is \(\displaystyle 2^k\)
Complexity: \(\displaystyle O(\log n)\) time and \(\displaystyle O(n\log n)\) work
Work-optimal List Ranking
- From our list A, pull a subset S with uniform density and sparcity
- Remove S from A, creating a new subset \(\displaystyle A-S\).
- For each element i in \(\displaystyle S\), fix the next and distance of prev(i)
- Run compaction
- Recurse on \(\displaystyle A-S\) until size is \(\displaystyle \leq n/\log n\). Then use pointer jumping.
- Add \(\displaystyle S\) back to \(\displaystyle A-S\)
- Complexity
We get the same complexity for randomized and deterministic list ranking (see below)
Randomized has the complexity with high probability.
- \(\displaystyle O(\log (n) \log \log (n))\) time
- \(\displaystyle O(n)\) work
Using a parallel prefix-sum algorith which runs in \(\displaystyle O(\log n/\log \log n)\) time, we can get list ranking in \(\displaystyle O(\log n)\) time and \(\displaystyle O(n)\) work.
Randomized Symmetry Breaking
for i 1 <= i <= n pardo
with equal probability R(i) = head or tail
if R(i) == HEAD and R(next(i))==Tail
s(i) = 0
else
s(i) = 1
- Notes
- The full randomized list ranking works in \(\displaystyle O(\log n \log\log n)\) time and \(\displaystyle O(n)\) work with high probability
Deterministic Symmetry Breaking
- Assign each element a unique tag, such as the index in the array
- Convert the tag to binary. For each element i, tag(i)!=tag(next(i)).
- Let k be the index of the rightmost bit (where 0 is the rightmost bit) differing between tag(i) and tag(next(i))
- Let b be the bit in tag(i) differing from tag(next(i))
- Set the new tag to
(k<<1) + b
This algorithm takes \(\displaystyle O(1)\) time and \(\displaystyle O(n)\) work per iteration.
If the range of tags before the iteration are \(\displaystyle [0,...,n-1]\) then the range of tags after will be \(\displaystyle [0,...,2*\log n - 1]\).
r-ruling set
An r-ruling set is a subset \(\displaystyle S\) of a linked list satisfying two properties:
- Uniform Density If node \(\displaystyle i\) is not in S, then one of the \(\displaystyle r\) nodes following i will be in \(\displaystyle S\)
- Uniform Sparcity If node \(\displaystyle i\) is in \(\displaystyle S\) then node \(\displaystyle next(i)\) is not in \(\displaystyle S\)
- Algorithm 1
The following algorithm gives us an r-ruling set with \(\displaystyle r=2*\log n - 1\)
- Apply the deterministic coin tossing algorithm to give each element a tag in \(\displaystyle [0,...,2*\log n - 1]\)
- For each element i in parallel, if i is a local maximum then add it to \(\displaystyle S\)
- Optimal-Work 2-Ruling set
Apply one iteration of deterministic coin tossing
Sort elements by tags
Initialize array S with 1s
for k = 0 to 2*log(n)-1:
for i such that tag(i) = k pardo
if S(pre(i)) = S(next(i)) = 1:
S(i) = 0
Tree Contraction
Serial Rake
Consider a node y with left leaf x and right subtree z.
Rake(x) would delete x and y, setting parent(z) to the previous parent of y.
Observation 1: Applying a rake to a binary tree yields a binary tree
Parallel Rake
Rake all leaves such that:
- No two leaves have the same parent (stem)
- The parent of a stem cannot be the stem of another leaf
Observation 2: Applying a legal parallel rake to a binary tree yields a binary tree
- Parallel Rake Contraction Scheme
Apply legal parallel rakes until the tree becomes a 3-node binary tree
- Parallel Rake Contraction Algorithm
- Step 1
- Number leaves according to a DFS using the Euler tour algorithm.
Observation 3:
Consider the leaves whose number is odd, L.
Let S consist of the stems of those leaves L.
Then each node in S can be adjacent to at most one other node in S.
Proof: See the classnotes
- Step 2
- Let \(\displaystyle S_1\) be nodes in \(\displaystyle S\) whose parents are not in \(\displaystyle S\).
- Let \(\displaystyle L_1\) be leaves in \(\displaystyle L\) whose parents are in \(\displaystyle S_1\).
- Apply parallel rakes to leaves in \(\displaystyle L_1\), unless the parent is the root.
- Apply parallel rakes to leaves in \(\displaystyle L - L_1\), unless the parent is the root.
- Repeat Step 2 until the tree is a 3-node binary tree
Complexity
Step 2 takes \(\displaystyle O(\log n)\) rounds. Each leaf gets raked only once.
In total we take \(\displaystyle O(\log n)\) time and \(\displaystyle O(n)\) work.
Evaluating an Arithmetic Expression
Consider a binary tree where each internal node is an operator:
Either addition or multiplication.
Each leaf is a number
Assign each internal node 4 numbers: a,b,c,d
These are initialized to (1,0,1,0)
The internal node will be \(\displaystyle (a*l+b) \times (c*r+d)\) where \(\displaystyle \times\) is either addition or multiplication.
If we delete one leaf and it's parent (stem), we will modify these variables of the stem's parent.
Tree Binarization
- Note
- This is not in the classnotes, but has been covered in exams.
To apply the above techniques to general trees or k-ary trees, you should binarize your k-ary tree.
This is done as follows:
- Suppose node \(\displaystyle x\) has \(\displaystyle n \gt 2\) children
- Select one child to keep
- Create a node \(\displaystyle x'\)
- Move all \(\displaystyle n-1\) children to \(\displaystyle x'\)
- Set child \(\displaystyle x'\) to be a child of \(\displaystyle x\)
Complexity
- The time is \(\displaystyle O(max\_degree)\) and the work is \(\displaystyle O(n)\)
Graph Connectivity
Preliminaries
For parallel algorithms, a graph can be represented as an incidence list or an adjacency matrix.
An incidence list is an array of edges ordered by the starting point and ending point. An array of vertices point to the starting index of the vertices outgoing edges within the edge array. I.e. edges with index [v[i], v[i+1]) start at vertex i
Definitions:
- Pointer Graph
- Supervertices
- The supervertex graph
- Hookings
- Parallel pointer jumping
A first connectivity algorithm
The first connectivity algorithm consists of \(\displaystyle \log(n)\) iterations of the following two steps:
- Hookings - Each root hooks itself the the minimal adjacent root. If there are no adjacent stars, then this rooted star quits.
- Parallel pointer jumping - Each vertex performs pointer jumping until every vertex points to the root, forming a rooted star.
- Theorems
- The pointer graph always consists of rooted trees.
- After \(\displaystyle \log n\) iterations, all vertices are contained in rooted stars that quit.
- Each connected component is represented by a single rooted star.
- Complexity
- We need \(\displaystyle O(\log n)\) iterations
- Hookings take \(\displaystyle O(1)\) time and \(\displaystyle O(n+m)\) work
- Pointer jumping takes \(\displaystyle O(\log n)\) time and \(\displaystyle O(n\log n)\) work
- For adjacency matrix, in total we need \(\displaystyle O(\log^2 n)\) time and \(\displaystyle O(n^2\log n)\) work since we have a processor per \(\displaystyle n^2\) possible edges.
- For incidence lists, we need \(\displaystyle O(\log^2 n)\) time and \(\displaystyle O(n\log^2 n + m\log n)\) work since we have a processor per edge.
A second connectivity algorithm
The second connectivity algorithms consists of \(\displaystyle O(\log n)\) iterations.
Each iteration takes constant time.
- Probe quitting: each rooted star whose supervertex is not adjacent to any other quits
- Hooking on smaller: each rooted star hooks onto a smaller vertex of another supervertex which is not a leaf
- Note that this is not unique. Requires arbitrary CRCW.
- Hooking non-hooked-upon: every rooted star not hooked upon in step 2 hooks to another vertex in another supervertex which is not a leaf
- Parallel pointer jumping: one round of parallel pointer jumping
- Theorems
- The pointer graph always consists of rooted trees.
- For every vertex which is not a leaf, \(\displaystyle D(v) \leq v\)
- This is true after steps 1, 2, and 4.
- This follows immediately for 1 and 2.
- After one round of pointer jumping (4) after 3, everyone from supervertex \(\displaystyle r\) is a leaf due to the claim below.
- Consider a root \(\displaystyle r\) which hooks on someone larger in step 3.
- After Step 3, all children of \(\displaystyle r\) are leaves.
- I.e. no one else will hook to \(\displaystyle r\) during Step 3.
- If anyone was larger, \(\displaystyle r\) would have hooked on them in Step 2.
- If anyone was smaller, they would have hooked on \(\displaystyle r\) in Step 2.
- Complexity
- Time \(\displaystyle O(\log n)\)
- Work \(\displaystyle O((n+m)\log n)\)
- Notes
- Without step 3, the algorithm will run in \(\displaystyle O(n)\) time instead of \(\displaystyle O(\log n)\) but the result will be valid.
- In step 2, you can hook rooted trees in addition to rooted stars for better empirical performance
Let \(\displaystyle h(T)\) be the height of tree T where a two-layer tree has height 1.
Define a single node to have height 1.
Let \(\displaystyle H\) be the sum of heights of all trees and \(\displaystyle \bar{H}\) be the total height after one iteration.
- Claim: \(\displaystyle \bar{H} \leq 2*H/3\)
Minimum Spanning Forest
The MSF Theorem
Let \(\displaystyle G(V,E)\) be a weighted graph and let \(\displaystyle U\) and \(\displaystyle V-U\) be two non-empty subsets of \(\displaystyle V\). Consider set \(\displaystyle H=\{(u,v) \mid u \in U, v \in V\}\) of edges connecting points in \(\displaystyle U\) and \(\displaystyle V\). If \(\displaystyle e\) is the edge of minimum weight in \(\displaystyle H\), then \(\displaystyle e\) is in the MSF of \(\displaystyle G\)
A first MSF algorithm
- Sort the edges by weight. Assign a processor to each edge. Using a priority CRCW, the edge with minimum weight will take priority during writes.
Each round consists of hooking and \(\displaystyle \log n\) rounds of parallel pointer jumping
- Each root find the minimum weight edge to another supervertex and hooks itself to that root.
- This is automatic from the priority CRCW.
A second MSF algorithm
We replace steps 2 and 3 in the connectivity algorithm with the simple rule:
- We hook rooted stars using the edge with the smallest weight.
- Notes
- The progression of edge weights up the tree are monotonically increasing so there are no cycles
Biconnectivity
This section is not it the textbook. It is from Tarjan and Vishkin (1985)[1].
A graph is biconnected if for every two vertices \(\displaystyle v_1\) and \(\displaystyle v_2\), there is a simple cycle containing \(\displaystyle v_1\) and \(\displaystyle v_2\). Intuitively this means that for any two vertices, there are at least two paths from \(\displaystyle v_1\) to \(\displaystyle v_2\). If any vertex and its edges are removed from a biconnected graph, it still remains connected.
Every connected graph consists of biconnected components. These are sets of edges such that every two edges from a set lie on a simple cycle. Vertices which connect two biconnected components are called articulation points. If these points are removed, the two biconnected components are no longer connected.
- Algorithm
Assume we are given a connected graph \(\displaystyle G\).
- First build a spanning tree \(\displaystyle T\). Record which edges are in the spanning tree. Root the spanning tree.
- Compute the preorder number of all edges using an euler tour.
- For every vertex \(\displaystyle v\), calculate the hi and low preorder numbers in the subtree \(\displaystyle T(v)\)
- Create the auxiliary graph \(\displaystyle G'' = (V'', E'')\) as follows:
- All edges of \(\displaystyle G\) are vertices in \(\displaystyle G''\)
- For each edge \(\displaystyle (v, w)\) in \(\displaystyle G - T\), add edge \(\displaystyle ((p(v),v),(p(w),w))\) to \(\displaystyle G''\) iff \(\displaystyle v\) and \(\displaystyle w\) are unrelated in \(\displaystyle T\)
- For each edge \(\displaystyle (v = p(w), w)\) in \(\displaystyle T\), add edge \(\displaystyle ((p(v), v), (v, w))\) to \(\displaystyle G''\) iff \(\displaystyle low(w) \lt v\) or \(\displaystyle high(w) \geq v + size(v)\)
- Compute the connected components of \(\displaystyle G''\)
- Assign edges based on their connected components.
- Complexity
- \(\displaystyle O(\log n)\) time
Tricks
Removing duplicates in an array
Assume you have an Arbitrary CRCW
- Given array A of size n with entries 0 to n-1
- For each entry pardo
- Write B[A[i]] == i
- Only one write will succeed for each unique A[i]
- Check if B[A[i]] == i
Compaction of an \(\displaystyle n^2\) array with \(\displaystyle \leq n\) elements in \(\displaystyle O(\log n)\) time
- Split our \(\displaystyle n^2\) array to n subarrays, each of size \(\displaystyle n\)
- Run \(\displaystyle n\) parallel compactions on each subarray
- Perform one compaction on the size of each subarray
- Compact all elements using (total size of prev subarrays + position in current subarray)
The benefit of this segmented compaction/prefix sum is that if you only do each segment once in an iterative algorithm such as parallel BFS, you can get \(\displaystyle O(n^2)\) or \(\displaystyle O(m)\) work.
XMT Programming Tips
I never figured out how to use standard c headers.
- XMT only has int (32 bit) and float (32 bit). If you need a bool type, you will need to define it in a header.
- You cannot call functions from within
spawn
Here is my helpers header helpers.h
helpers.h#ifndef HELPERS_H
#define HELPERS_H
#define true 1
#define false 0
#define bool int
// #define NIL -1
#define max(a, b) ((((a) < (b)) ? (b) : (a)))
#define min(a, b) ((((a) < (b)) ? (a) : (b)))
#endif
If you prefer to debug in C++ like me, you can use the following code to adapt running the XMT code: This code does not run things asynchronously.
#define spawn(x, y) for (int $ = x; $ <= y; ++$)
//#define spawn(x, y) for (int $ = y; $ >= x; --$)
#define ps(a, b) \
{ \
b += a; \
a = b - a; \
}
#define psm(a, b) \
{ \
b += a; \
a = b - a; \
}
#define psBaseReg int
#define STRINGIFY2(X) #X
#define STRINGIFY(X) STRINGIFY2(X)
using namespace std;
#define GRAPH_NUM graph0
#define N 19
#define M 36
vector<int> vertices;
vector<int> degrees;
vector<vector<int>> edges;
int main() {
vertices.resize(N);
degrees.resize(N);
edges = std::vector<std::vector<int>>(M, std::vector<int>(2));
string datapath = "data/" STRINGIFY(GRAPH_NUM) "/graph.txt";
string data = readFile(datapath);
regex section_regex(
"[\\n\\r][\\n\\r]+|[\\r\\n]0\\s[\\r\\n]+",
std::regex_constants::ECMAScript | std::regex_constants::icase);
regex space_regex("[\\n\\s\\r]+", std::regex_constants::ECMAScript |
std::regex_constants::icase);
vector<string> sections = split(data, section_regex);
// for (int i = 0; i < sections.size(); i++) {
// cout << "Section " << i << " " << sections[i].size() << endl;
// cout << sections[i] << endl;
//}
return 0;
}
string readFile(const string& datapath) {
std::ifstream in(datapath, std::ios::in);
string data;
if (in.good()) {
std::string contents;
in.seekg(0, std::ios::end);
contents.resize(static_cast<unsigned int>(in.tellg()));
in.seekg(0, std::ios::beg);
in.read(&contents[0], contents.size());
return contents;
}
std::cerr << "Failed to open file: " << datapath << std::endl;
throw(errno);
}
vector<string> split(string s, regex r) {
vector<string> splits;
smatch m; // <-- need a match object
while (regex_search(s, m, r)) // <-- use it here to get the match
{
int split_on = m.position(); // <-- use the match position
splits.push_back(s.substr(0, split_on));
s = s.substr(split_on + m.length()); // <-- also, skip the whole match
}
if (!s.empty()) {
splits.push_back(s); // and there may be one last token at the end
}
return splits;
}
Hardware/Architecture
Models for Advancing PRAM and Other Algorithms into Parallel Algorithms for PRAM
- MTCU - Master Thread Control Unit - runs in serial mode
- TCU Cluster - Thread Control Unit
- Procedure
- Spawn broadcasts your spawn code in the block to every thread control unit (TCU).
- Data is shared through the interconnection network
- Performance Penalty
\(\displaystyle \text{Execution Depth} = \text{Computation Depth} + LSRTM \times R + QD\)
- \(\displaystyle LSTRM\) - length of sequence of round trips to memory
- \(\displaystyle R\) - time for round trip to memory
- \(\displaystyle QD\) - queuing delay
- If multiple threads access the same memory module, they are queued at the memory module
Resources
Textbooks
- Uzi Vishkin ENEE651/CMSC751 Classnotes
- Introduction to Parallel Algorithms (Joseph Jaja, textbook)
- Parallel Algorithms by Guy E. Blelloch and Bruce M. Maggs (CMU)
References
- ↑ Robert E. Tarjan, and Uzi Vishkin. An Efficient Parallel Biconnectivity Algorithm (1985). SIAM Journal on Computing. DOI: 10.1137/0214061 https://epubs.siam.org/doi/10.1137/0214061 Mirror