Neural RGB→D Sensing: Depth and Uncertainty from a Video Camera
Appearance
Neural RGB→D Sensing: Depth and Uncertainty from a Video Camera (CVPR 2019)
Authors: Chao Liu, Jinwei Gu, Kihwan Kim, Srinivasa G. Narasimhan, Jan Kautz
Affiliations: NVIDIA, Carnegie Mellon University, SenseTime
The main ideas here are:
- Estimate a "depth probability distribution" rather than a single value
- For each image, we get a "Depth Probability Volume (DPV)" representing a depth MLE and an uncertainty measure.
- Accumulate DPV estimates across time or across frames.
Method
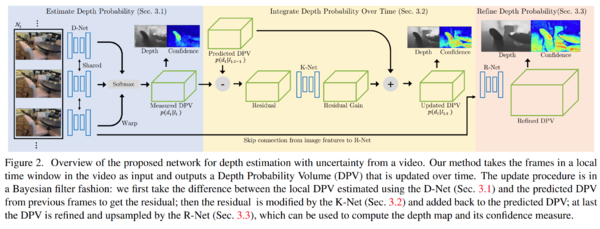
- They first estimate the DPV using a network called the D-Net.
- Next they calculate the difference between the current predicted DPV and the previous DPV.
- This residual is passed through the K-Net to create an update.
- The update is added to the previous DPV to create the updated DPV.
- An R-Net refines the updated DPV using input image features from the D-Net.
Architecture
See their supplementary material for details.
D-Net
The D-Net consists of 28 convolutional blocks followed by 4 branches of spatial pyramid layers and a fusion layer.
