Light Field Duality: Concept and Applications: Difference between revisions
Created page with "Light Field Duality: Concept and Applications Authors: George Chen, Li Hong, Kim Ng, Peter McGuinness, Christian Hofsetz, Yang Liu, Nelson Max Affiliations: STMicroelectronic..." |
No edit summary |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Light Field Duality: Concept and Applications | Light Field Duality: Concept and Applications (VRST 2002) | ||
Authors: George Chen, Li Hong, Kim Ng, Peter McGuinness, Christian Hofsetz, Yang Liu, Nelson Max | Authors: George Chen, Li Hong, Kim Ng, Peter McGuinness, Christian Hofsetz, Yang Liu, Nelson Max | ||
Affiliations: STMicroelectronics, UC Davis | Affiliations: STMicroelectronics, UC Davis | ||
* [https://dl.acm.org/doi/abs/10.1145/585740.585743 ACM DL] [https://dl.acm.org/doi/pdf/10.1145/585740.585743 ACL DL PDF] [https://escholarship.org/content/qt0fp8x522/qt0fp8x522.pdf escholorship.org mirror] | |||
==Background== | |||
A light field is the set of all rays in a 2D space. It is a 5D function of <math>(x,y,z)</math> position and <math>(\theta, \phi)</math> angle. | |||
However for practical scenes, you can assume that the light along a ray is consistent through empty spaces (air). | |||
Thus it can be represented in 4D as either a position <math>(u, v)</math> on a fixed plane and an angle <math>(\theta, \phi)</math> or as two positions <math>(u, v)</math> and <math>(s, t)</math> on two nearby parallel planes. | |||
See [[Light field]]. | |||
==Dual Representation== | ==Dual Representation== | ||
[[File:Light field duality fig1.png|thumb|400px]] | |||
The paper forms the dual representation between points in 3D world coordinates and hyperlines in the 2-plane 4D parameterization of light fields. | The paper forms the dual representation between points in 3D world coordinates and hyperlines in the 2-plane 4D parameterization of light fields. | ||
By hyperline, they mean a 2D manifold in 4D space that is the intersection of two 4D hyperplanes. | By hyperline, they mean a 2D manifold in 4D space that is the intersection of two 4D hyperplanes. | ||
The duality is defined as follows: | |||
Given a 3D point <math>P=(x,y,z)</math>, any ray <math>(s,t,u,v)</math> going through P would have: | |||
<math> | |||
\frac{s-x}{u-x} = \frac{t-y}{v-y} = \frac{z-z_{st}}{z-z_{uv}} | |||
</math> | |||
where <math>z_{st}</math>, <math>z_{uv}</math> are fixed values. | |||
See the figure to the right. | |||
With some algebra, this constraint can be written as either: | |||
<math> | |||
\begin{bmatrix} | |||
z_{uv}-z_{st} & 0 & s-u\\ | |||
0 & z_{uv} - z_{st} & t-v | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
x \\ y \\ z | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
sz_{uv} - uz_{st}\\ | |||
tz_{uv} - vz_{st}\\ | |||
\end{bmatrix} | |||
</math> | |||
Or: | |||
<math> | |||
\begin{bmatrix} | |||
z-z_{uv} & 0 & z_{st}-z & 0\\ | |||
0 & z-z_{uv} & 0 & z_{st} - z | |||
\end{bmatrix} | |||
\begin{bmatrix}s \\ t \\ u \\ v \end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
x(z_{st}-z_{uv})\\ | |||
y(z_{st}-z_{uv}) | |||
\end{bmatrix} | |||
</math> | |||
Given a point, this constraint defines the hyperline in the 4D light field space. | |||
Henceforth, a hyperline will be represented as <math>(a, b, c, d)</math> where hyperpoints on said line satisfy: | |||
<math> | |||
\begin{bmatrix} | |||
a & 0 & b & 0\\ | |||
0 & a & 0 & b | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
s \\ t \\ u \\ v | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
c \\ d | |||
\end{bmatrix} | |||
</math> | |||
The paper has the following remarks: | |||
* Points in one space are lines in the other. | |||
* A bundle of lines in world space correspond to a set of hyperlinear points in the light field. | |||
* A set of colinear points in world space corresponds to a bundle of hyperlines in the light field. | |||
In the light field space, you get: | |||
* Camera hyperlines (CHL) which correspond to camera points in world space. Hyperpoints along the hyperline have heterogenous colors since they represent images. | |||
* Geometry hyperlines (GHL) which correspond to points in the scene (on surfaces) in world space. Hyperpoints along these hyperlines have homogeneous colors assuming no view dependent effects. | |||
==CHL Light Field Rendering== | |||
Each camera <math>i</math> is a point in world coordinates which corresponds to a hyperline <math>\mathbf{l}_i=(a_i, b_i, c_i, d_i)</math> in the light field. | |||
If we want to render from a new viewpoint, for each render pixel, we have a target ray which corresponds a point on the light field <math>\mathbf{r} = (s_r, t_r, u_r, v_r)</math>. | |||
For each camera/hyperline <math>i</math>, you can find the ray/hyperpoint which minimizes some distance function: | |||
<math> | |||
\begin{aligned} | |||
d^2 &= \Vert (s_i,t_i,u_i,v_i) - (s_r,t_r,u_r,v_r) \Vert^2_2\\ | |||
&= (s_i - s_r)^2 + (t_i - t_r)^2 + (u_i - u_r)^2 + (v_i - v_r)^2 | |||
\end{aligned} | |||
</math>. | |||
There is a closed form solution provided in the paper. | |||
Then simply blend with weights as inverse distance. | |||
===Dynamic focal plane=== | |||
You can add a slope loss to the distance function to make sure rays point in the same direction: | |||
<math> | |||
\begin{aligned} | |||
d^2 &= \Vert (s_i,t_i,u_i,v_i) - (s_r,t_r,u_r,v_r) \Vert^2_2 +\\ | |||
&\hspace{5mm}\beta\Vert (s_i-u_i, t_i-v_i) - (s_r-u_r, t_r-v_r) \Vert^2_2 | |||
\end{aligned} | |||
</math>. | |||
If the virtual camera is not at the same position as the source cameras, then the lines will not be parallel and will intersect. | |||
<math>\beta</math> can be used to control the depth at which they intersect. | |||
==GHL Light Field Rendering== | |||
Rendering lightfields using geometry hyperlines is equivalent to rendering point clouds. | |||
For each virtual ray, you can compute the dual <math>(s_r, t_r, u_r, v_r)</math>. | |||
Then for each GHL, you can compute the optimal ray closest to the virtual ray. | |||
Then blend over selected GHLs. | |||
The paper has details on addressing issues with holes and opacity using clustering. | |||
Latest revision as of 19:57, 13 January 2021
Light Field Duality: Concept and Applications (VRST 2002)
Authors: George Chen, Li Hong, Kim Ng, Peter McGuinness, Christian Hofsetz, Yang Liu, Nelson Max Affiliations: STMicroelectronics, UC Davis
Background
A light field is the set of all rays in a 2D space. It is a 5D function of \(\displaystyle (x,y,z)\) position and \(\displaystyle (\theta, \phi)\) angle. However for practical scenes, you can assume that the light along a ray is consistent through empty spaces (air). Thus it can be represented in 4D as either a position \(\displaystyle (u, v)\) on a fixed plane and an angle \(\displaystyle (\theta, \phi)\) or as two positions \(\displaystyle (u, v)\) and \(\displaystyle (s, t)\) on two nearby parallel planes. See Light field.
Dual Representation
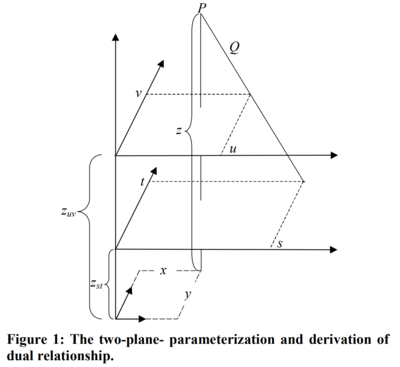
The paper forms the dual representation between points in 3D world coordinates and hyperlines in the 2-plane 4D parameterization of light fields.
By hyperline, they mean a 2D manifold in 4D space that is the intersection of two 4D hyperplanes.
The duality is defined as follows:
Given a 3D point \(\displaystyle P=(x,y,z)\), any ray \(\displaystyle (s,t,u,v)\) going through P would have:
\(\displaystyle
\frac{s-x}{u-x} = \frac{t-y}{v-y} = \frac{z-z_{st}}{z-z_{uv}}
\)
where \(\displaystyle z_{st}\), \(\displaystyle z_{uv}\) are fixed values.
See the figure to the right.
With some algebra, this constraint can be written as either:
\(\displaystyle
\begin{bmatrix}
z_{uv}-z_{st} & 0 & s-u\\
0 & z_{uv} - z_{st} & t-v
\end{bmatrix}
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
=
\begin{bmatrix}
sz_{uv} - uz_{st}\\
tz_{uv} - vz_{st}\\
\end{bmatrix}
\)
Or:
\(\displaystyle
\begin{bmatrix}
z-z_{uv} & 0 & z_{st}-z & 0\\
0 & z-z_{uv} & 0 & z_{st} - z
\end{bmatrix}
\begin{bmatrix}s \\ t \\ u \\ v \end{bmatrix}
=
\begin{bmatrix}
x(z_{st}-z_{uv})\\
y(z_{st}-z_{uv})
\end{bmatrix}
\)
Given a point, this constraint defines the hyperline in the 4D light field space.
Henceforth, a hyperline will be represented as \(\displaystyle (a, b, c, d)\) where hyperpoints on said line satisfy:
\(\displaystyle
\begin{bmatrix}
a & 0 & b & 0\\
0 & a & 0 & b
\end{bmatrix}
\begin{bmatrix}
s \\ t \\ u \\ v
\end{bmatrix}
=
\begin{bmatrix}
c \\ d
\end{bmatrix}
\)
The paper has the following remarks:
- Points in one space are lines in the other.
- A bundle of lines in world space correspond to a set of hyperlinear points in the light field.
- A set of colinear points in world space corresponds to a bundle of hyperlines in the light field.
In the light field space, you get:
- Camera hyperlines (CHL) which correspond to camera points in world space. Hyperpoints along the hyperline have heterogenous colors since they represent images.
- Geometry hyperlines (GHL) which correspond to points in the scene (on surfaces) in world space. Hyperpoints along these hyperlines have homogeneous colors assuming no view dependent effects.
CHL Light Field Rendering
Each camera \(\displaystyle i\) is a point in world coordinates which corresponds to a hyperline \(\displaystyle \mathbf{l}_i=(a_i, b_i, c_i, d_i)\) in the light field.
If we want to render from a new viewpoint, for each render pixel, we have a target ray which corresponds a point on the light field \(\displaystyle \mathbf{r} = (s_r, t_r, u_r, v_r)\).
For each camera/hyperline \(\displaystyle i\), you can find the ray/hyperpoint which minimizes some distance function:
\(\displaystyle
\begin{aligned}
d^2 &= \Vert (s_i,t_i,u_i,v_i) - (s_r,t_r,u_r,v_r) \Vert^2_2\\
&= (s_i - s_r)^2 + (t_i - t_r)^2 + (u_i - u_r)^2 + (v_i - v_r)^2
\end{aligned}
\).
There is a closed form solution provided in the paper.
Then simply blend with weights as inverse distance.
Dynamic focal plane
You can add a slope loss to the distance function to make sure rays point in the same direction:
\(\displaystyle
\begin{aligned}
d^2 &= \Vert (s_i,t_i,u_i,v_i) - (s_r,t_r,u_r,v_r) \Vert^2_2 +\\
&\hspace{5mm}\beta\Vert (s_i-u_i, t_i-v_i) - (s_r-u_r, t_r-v_r) \Vert^2_2
\end{aligned}
\).
If the virtual camera is not at the same position as the source cameras, then the lines will not be parallel and will intersect.
\(\displaystyle \beta\) can be used to control the depth at which they intersect.
GHL Light Field Rendering
Rendering lightfields using geometry hyperlines is equivalent to rendering point clouds.
For each virtual ray, you can compute the dual \(\displaystyle (s_r, t_r, u_r, v_r)\).
Then for each GHL, you can compute the optimal ray closest to the virtual ray.
Then blend over selected GHLs.
The paper has details on addressing issues with holes and opacity using clustering.
