SURF: Speeded Up Robust Features: Difference between revisions
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
* [https://link.springer.com/chapter/10.1007/11744023_32 Springer Link to Paper (ECCV 2006) Paywall] | |||
* [http://people.ee.ethz.ch/~surf/eccv06.pdf Paper] | |||
* [[Media:Surf_speeded_up_robust_features_eccv06.pdf | Mirror]] | |||
* | ;Authors: | ||
* Herbert Bay - ETH Zurich | |||
* Tinne Tuytelaars - Katholieke Universiteit Leuven | |||
* Luc Van Gool - ETH Zurich, Katholieke Universiteit Leuven | |||
==Feature Extraction== | ==Feature Extraction== | ||
| Line 7: | Line 13: | ||
Our features will be regions in the image where the determinant of the Hessian are local maxima. | Our features will be regions in the image where the determinant of the Hessian are local maxima. | ||
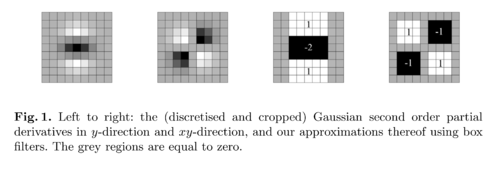
[[File:surf_fig_1.png | thumb | 500px | Figure 1 from the paper. Each region can be computed using a summed area table/integral image.]] | |||
* The Hessian matrix: | * The Hessian matrix: | ||
<math>\mathcal{H}(\mathbf{x}, \sigma) | <math>\mathcal{H}(\mathbf{x}, \sigma) | ||
| Line 14: | Line 22: | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
* Each entry is a convolution of a the Gaussian second order derivative with the image at <math>\mathbf{x}</math> | * Each entry is a convolution of a the Gaussian second order derivative with the image at <math>\mathbf{x}</math> | ||
* These convolutions are approximated using box filters on an integral image. | * These convolutions are approximated using box filters on an integral image (Fig 1). | ||
*: The approximations are denoted as <math>D_{xx}, D_{yy}, D_{xy}</math> | *: The approximations are denoted as <math>D_{xx}, D_{yy}, D_{xy}</math> | ||
* The determinant of the hessian is then <math>D_{xx}D_{yy} - (0.9*D_{xy})^2</math> | * The determinant of the hessian is then <math>D_{xx}D_{yy} - (0.9*D_{xy})^2</math> | ||
| Line 33: | Line 41: | ||
===Orientation Assignment=== | ===Orientation Assignment=== | ||
[[File:Surf fig 2.png | thumb | 500px | Figure 2 from the paper]] | |||
* Sample Haar-wavelet responses in x and y-direction at points around each feature | * Sample Haar-wavelet responses in x and y-direction at points around each feature | ||
** Using integral images, only 6 operations are need to compute in x or y direction | ** Using integral images, only 6 operations are need to compute in x or y direction (Fig. 2 middle) | ||
**: We have 6 distinct corners so we need | **: We have 6 distinct corners so we need 6 fma operations in total for each direction. (Actually 5 if one value is just multiplied by 1) | ||
* Using a 360-degree (pivoting) sliding window with radius <math>\frac{\pi}{3}</math>, calculate the sum of all horizontal and vertical responses yielding vector. Note the window moves in increments of <math>\frac{\pi}{3}</math> | * Using a 360-degree (pivoting) sliding window with radius <math>\frac{\pi}{3}</math>, calculate the sum of all horizontal and vertical responses yielding vector. Note the window moves in increments of <math>\frac{\pi}{3}</math> | ||
* Pick the direction with the largest vector. | * Pick the direction with the largest vector. | ||
===Descriptor Components=== | ===Descriptor Components=== | ||
* Create square regions positioned at feature points and oriented using the calculated orientation | * Create square regions positioned at feature points and oriented using the calculated orientation (Fig. 2 right) | ||
* ... | * ... | ||
==OpenCV== | |||
SURF is available in OpenCV | |||
==Resources== | ==Resources== | ||
* [https://medium.com/data-breach/introduction-to-surf-speeded-up-robust-features-c7396d6e7c4e Medium Introduction] | * [https://medium.com/data-breach/introduction-to-surf-speeded-up-robust-features-c7396d6e7c4e Medium Introduction] | ||